Kalkulator For Differensial girforhold
Innholdsfortegnelse
- Innledning
- startverdi for girforholdet
- endelig verdi for girforholdet
- Korreksjon For Girforhold
- Logisk diagram
- Eksempel for et forbrenningskjøretøy
- Eksempel for et elektrisk kjøretøy
- Kalkulator
Introduksjon
denne artikkelen forklarer ikke hvordan du beregner girforholdet for et gitt sett med gir. Hvis du vil vite hvordan du beregner girforholdet for et gitt par gir, les artikkelen hvordan beregne du et girforhold ?
Denne artikkelen forklarer hvordan girforholdet for differensialet er valgt / beregnet / bestemt for et gitt kjøretøy, som vi vet visse parametere for.
når du designer drivverket til et nytt kjøretøy, uansett om det drives av en forbrenningsmotor eller en elektrisk maskin, må vi bestemme hvilket girforhold vi skal ha på differensialet (også kalt final drive).
hvis du sjekker forskjellige kjøretøy, ser du at de har forskjellige girforhold for differensial. Noen eksempler er beskrevet i tabellen nedenfor:
| Kjøretøy | Maksimal hastighet | Hjulstørrelse | Motor/motorhastighet @ maks effekt |
toppgir | siste girforhold |
| 19MY BMW M2 | 280 | 265/35 ZR 19 98Y | 6250 | 0.85 | 3.46 |
| 21 MIN Ford Mustang Mach-E | 180 | 225/60R18 | 12000 | 1.00 | 9.05 |
DATAENE FOR BMW ble hentet fra carfolio.com. dataene Til Ford Mustang Mach-E ble hentet fra ulike kilder på internett. Maksimal motorhastighet er en tilnærming, alle andre data leveres av produsenten.
Som du kan se, er det forskjellige verdier for girforholdet til differensialet. Spørsmålet som vi skal prøve å svare på er: Hvilket utvekslingsforhold skal min differensial ha? Svaret på dette spørsmålet kommer fra fysikk, det er ikke et gjetning.
for å beregne girforholdet til differensialet må vi vite følgende:
- kjøretøyets maksimale hastighet
- hjulets rullende radius
- motorhastigheten for maksimal effekt (hvis kjøretøyet drives av en forbrenningsmotor) eller motorens maksimale hastighet (i tilfelle et elektrisk kjøretøy)
- giret (siste gir på girkassen) der maksimal hastighet oppnås (dette er vanligvis toppgiret for kjøretøy med høy dynamisk ytelse eller giret). før top gear for de fleste kjøretøy)
bilens maksimale hastighet er en forhåndsinnstilt verdi, det er et designmål. Vanligvis, når en produsent designer et nytt kjøretøy, vil det definere hva som er topphastigheten.
rulleradiusen kan tilnærmes ved å bruke dekksymbolet (f. eks. 225 / 60R18). For å forstå hvordan du beregner rulleradius fra dekksymbolet, les artikkelen slik beregner du hjulradius.
hvis kjøretøyet drives av en forbrenningsmotor, må vi kjenne egenskapene til motoren når det gjelder motorhastighet ved maksimal effekt. Dette er nødvendig fordi maksimal hastighet oppnås når motoren spinner med maksimal effekt(vanligvis 5% over maksimal effekthastighet). Vi antar også at vi vet i hvilket gir av girkassen maksimal hastighet er oppnådd.

Bilde: Kriterier For Maksimal hastighet funksjon av kraft og veibelastning-forbrenningsmotor |
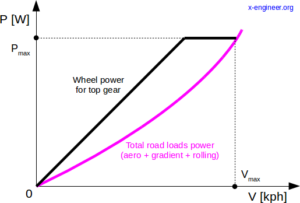
Bilde: Maksimal hastighet kriterier funksjon av kraft og veibelastning-elektrisk motor |
hvis kjøretøyet drives av en elektrisk motor, oppnås maksimal kjøretøyhastighet ved maksimal elektrisk motorhastighet. En annen forskjell å legge merke til er at, vanligvis, elektrisk kjøretøy har bare ett gir reduksjon, som er en på differensial (siste stasjon). Siden dagens elbil ikke har multi-trinns girkasser, top gear finnes ikke derfor i vår beregningsmetode vil vi vurdere forholdet til å være 1.00(som betyr at det ikke har noen innflytelse på hastighet og dreiemoment).
hovedforutsetningen ved beregning av differensialgirforholdet er at maksimal kjøretøyhastighet oppnås ved maksimal motorhastighet (ICE) eller maksimal motorhastighet (elektrisk motor). Fra denne antagelsen kan vi tegne en forenklet kinematisk skjematisk av drivverket.

Bilde: beregning av differensial girforhold – kinematisk skjematisk
hvor:
NPmax – er motorturtallet ved maksimal effekt
Ix – girforhold (girkasse) av det innkoblede giret
i0 – differensialgirforhold
nin – inngangshastighet på differensialet
nout – utgangshastighet på differensialet
NVmax – hjulhastighet ved maksimal kjøretøyhastighet
Observasjon: i tilfelle av elektriske biler (EV) paret av gir som danner ix-utvekslingsforholdet eksisterer ikke. Utgangen fra den elektriske motoren er koblet direkte til differensialinngangsakselen.
Gå tilbake
Initial verdi av girutvekslingen
Siden det er en mekanisk forbindelse mellom motor/motor og hjulet, uten slip, og forutsatt at kjøretøyet er på en rett vei, kan vi skrive hastighet balanse av differensial:
\
differensial inngangshastigheten kan skrives funksjon av motorturtall og engasjert gear av girkassen:
\
også differensialutgangshastigheten Er Lik hjulhastigheten (forutsatt ingen dekkslip):
\
hjulets rotasjonshastighet kan skrives funksjon av kjøretøyets hastighet og hjulradius:
\
Bytte (4) i (3) og deretter (2) og (3) i (1) gir:
\
som diskutert før, vil vi vurdere at i tilfelle av et kjøretøy drevet av en forbrenningsmotor, oppnås maksimal hastighet på kjøretøyet med en hastighet høyere enn maksimal effekthastighet. Derfor vil vi introdusere en maksimal hastighetskoeffisient cNmax som vil bli multiplisert med NPmax.
\
fra (6) kan vi trekke ut ligningen som beregner det første differensialgirforholdet:
\{i_{0i} = \frac{c_{Nmax} \cdot N_{Pmax} \cdot r_{w}}{2.6526 \cdot i_{x} \cdot V_{max}} \tag{7}\]
Gå tilbake
Endelig verdi av girforholdet
Ligning (7) gir den teoretiske (innledende, rå) verdien av differensial girforholdet. Den faktiske (endelige) girforholdet beregnes ut fra antall tenner på girnettet. For å beregne dette må vi først sette antall tenner på inngangsgiret (pinion) zIN .
minste antall tenner for inngangsgiret avhenger av typen gir som brukes til differensialet.

Bilde: Hypoid skråkant utstyr |

Bilde: Parallell akse spiralformet gir |
avhengig av utformingen av drivverket, biler har forskjellige gir sett for differensial:
- langsgående motor/motorvogner har hypoidkantgir, på grunn av at aksen til girkassens utgangsaksel er vinkelrett på drivakselens akse
- transversale motor/motorvogner har spiralformede gir, på grunn av at aksen til girkassens utgangsaksel er parallell med drivakselens akse
generelt har kjøretøy med forbrenningsmotorer begge hypoidkanter og spiralformede tannhjul, avhengig av plassering og motorfeste. Elektriske kjøretøy har imidlertid parallelle akse spiralformede gir for differensial siden aksen av motoren er parallell med aksen av drivakselen.
for hypoid skrågiret avhenger det minste antall tenner av verdien av girforholdet . Inngangsgiret kalles tannhjul og har mindre tenner enn utgangsgiret.
| i0 | 2.5 | 3 | 4 | 5 | 6-7 | >7 |
| zIN | *15 | *12 | 9 | 7 | 5 | 5 |
* for girforhold under 3 kan tannhjulsgiret ha 11 tenner eller mer
for tannhjulsgir, minim antall tenner på inngangsgiret kan være et hvilket som helst tall mellom 14 – 17 . I tilfelle av elektriske biler, hvis det endelige girforholdet er høyt (> 10,00), kan den enkle girmekanismen deles inn i to-trinns girtog. Dette gjøres vanligvis for å begrense størrelsen på utgangsgiret.

Bilde: totrinns tannhjulsgir – 3 parallelle akser |

Bilde: totrinns tannhjulsgir – 2 konsentriske akser |
i tilfelle av to-trinns girsett, vil det totale girforholdet være produktet mellom de mellomliggende girforholdene:
\
for enkelhet, i våre beregningseksempler skal vi bare vurdere enkle girsett for differensialet.
antall tenner på differensialgirene er bare et grovt estimat (startverdier). Det endelige tallet vil avhenge av flere faktorer som: geometri, størrelse, pålitelighet, produksjonsprosess, etc.
etter å ha bestemt typen girsett, kan vi velge antall tenner for inngangsgiret. Som eksempel kan vi velge flere verdier, for eksempel:
\
det neste trinnet er å beregne antall tenner på utgangsgiret, som er produktet mellom antall tenner på inngangsgiret og innledende girforhold for differensialet.
\
Ligning (9) vil gi et reelt tall for antall tenner på utgangsgiret. Vi må runde dette nummeret til nærmeste heltall. For eksempel hvis zOUT = 73.234 det vil bli avrundet til 73, hvis zOUT = 81.74 det vil bli avrundet til 82.
Gå tilbake
Girutvekslingskorreksjon
siden zOUT vil være forskjellig fra den opprinnelige beregnede verdien, må vi beregne girutvekslingsforholdet med den avrundede verdien av zOUT.
\
med det omberegnede girforholdet kan vi også beregne kjøretøyets maksimale hastighet for å se avvikene fra startverdien. Hvis vi ombestiller ligning (7), får vi uttrykket for maksimal hastighet som:
\
for å sikre at maksimalhastighetskravet er oppfylt, vil vi bare bringe frem girforholdene som maksimalhastigheten er nådd eller overskredet.
de endelige kriteriene for girutvekslingsberegningen er den relative feilen mellom den opprinnelige verdien av girutvekslingen og de endelige verdiene etter avrunding av zOUT.
\} \ tag{12}\]
girforholdet som har den minste relative feilen, skal velges som endelig verdi for differensialet (endelig stasjon).
Gå tilbake
Logisk diagram
alle trinnene for beregning av differensial girforhold er oppsummert i det logiske diagrammet nedenfor.
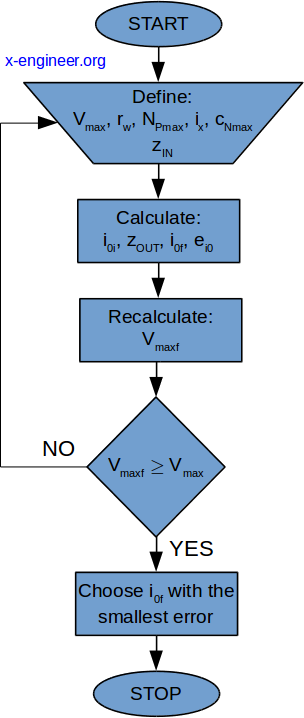
Bilde: beregning av differensial girforhold-logisk diagram
Gå tilbake
Eksempel på et forbrenningskjøretøy
FOR BMW-kjøretøyet fra tabellen ovenfor la oss beregne det endelige drivforholdet (differensial) basert på inngangsdataene. Siden vi har den reelle girutvekslingsverdien som allerede er oppgitt, kan vi sammenligne den med vår beregnede verdi for å validere beregningsprosessen.
Trinn 1. Beregn hjulradius, se artikkelen hvordan beregne hjulradius for detaljer.
\
Trinn 2. Beregn det opprinnelige girforholdet ved hjelp av ligning (7).
\
som du kan se den opprinnelige beregnede verdien av 3.472 er svært nær produsentens verdi på 3.46.
Trinn 3. Sett 4 verdier for antall tenner for inngangsgiret (tannhjul).
\
Trinn 4. Beregn antall tenner for utgangsgiret ved hjelp av ligning (9) og rund mot nærmeste heltall.
\
Trinn 5. Beregne differensial girforhold ved hjelp av ligningen (10).
\
Trinn 6. Beregn maksimal kjøretøyhastighet ved hjelp av ligning (11) og rund mot nærmeste heltall.
\
Som du kan se, for girforholdet på 3.5 maksimal hastighet er under det opprinnelige målet på 280 km / t. Av denne grunn kommer vi ikke til å vurdere utvekslingsforholdet på 3,5 for vår endelige beslutning.
Trinn 7. Beregn den relative feilen i de endelige girforholdene 3,455 og 3,462 sammenlignet med den opprinnelige verdien på 3,472 ved hjelp av ligning (12).
\
den minste feilen er for girforholdet på 3.462, derfor vil det bli valgt for kjøretøyet som en designparameter.
Trinn 8. Oppgi de endelige parametrene for utvekslingsforholdet.
\
som du kan se vår beregnede verdi (opp til andre desimal) er nøyaktig den samme som den som tilbys av produsenten som viser at beregningsmetoden er riktig.
Observasjon: denne beregningsmetodikken tar i hovedsak hensyn til maksimalhastighetskriteriene og noen girgeometriskriterier. I virkeligheten kan beslutningen om antall tenner for girsettet ta hensyn til andre faktorer som: produksjon, slitasje,pålitelighet, geometri, etc. og det endelige resultatet av utvekslingsforholdet kan variere.
Gå tilbake
Eksempel på et elektrisk kjøretøy
For Ford mach-e-kjøretøyet fra tabellen ovenfor la oss beregne det endelige drivforholdet (differensial) basert på inngangsdataene. Siden vi har den reelle girutvekslingsverdien som allerede er oppgitt, kan vi sammenligne den med vår beregnede verdi for å validere beregningsprosessen.
Trinn 1. Beregn hjulradius, se artikkelen hvordan beregne hjulradius for detaljer.
\
Trinn 2. Beregn det opprinnelige girforholdet ved hjelp av ligning (7).
\
Som du kan se den opprinnelige beregnede verdien av 9.148 er relativt nær produsentens verdi på 9.050.
Trinn 3. Sett 4 verdier for antall tenner for inngangsgiret (tannhjul).
\
Trinn 4. Beregn antall tenner for utgangsgiret ved hjelp av ligning (9) og rund mot nærmeste heltall.
\
Trinn 5. Beregne differensial girforhold ved hjelp av ligningen (10).
\
Trinn 6. Beregn maksimal kjøretøyhastighet ved hjelp av ligning (11) og rund mot nærmeste heltall.
\
som du kan se, for girforholdet på 9.176 er maksimal kjøretøyhastighet under det første målet på 180 km / t. Av denne grunn skal vi ikke vurdere utvekslingsforholdet på 9.176 for vår endelige beslutning.
Trinn 7. Beregn den relative feilen til de endelige girforholdene på 9,143, 9,133, 9,125 og sammenlignet med den opprinnelige verdien på 9,148 ved hjelp av ligning (12).
\
den minste feilen er for girforholdet 9.143, derfor vil det bli valgt for kjøretøyet som en designparameter.
Trinn 8. Oppgi de endelige parametrene for utvekslingsforholdet.
\
som du kan se vår beregnede verdi av girforholdet er relativt nærmere den som er publisert av produsenten.
Gå tilbake
Kalkulator
du kan prøve forskjellige parametere av kjøretøyet og få differensial girforhold ved hjelp av kalkulatoren nedenfor.
| Vmax | rw | ix | NPmax | cNmax |
| Beregn girutveksling | i0i = 2.802 | |||
| zIN1 = | zOUT1 = 25 | i01f = 2.778 | ei01 = 0,864 | Vmaxf1 = 252.2 |
| zIN2 = | zOUT2 = 31 | i02f = 2,818 | ei02 = 0,578 | Vmaxf2 = 248.6 |
| zIN1 = | zOUT3 = 36 | i03f = 2,769 | ei03 = 1,169 | Vmaxf3 = 253.0 |
En Scilab script som automatisk beregner differensial girforhold er tilgjengelig På Patreon siden.
Gå tilbake