• Articles
• admin

• Alfa de Cronbach – Definição Rápida
• SPSS Alfa de Cronbach de Saída
• Aumento de Alfa de Cronbach Removendo Itens
• Alfa de Cronbach é Negativo
• Há muito Poucos Casos (N = 0) para a Análise
• APA Relatório Alfa de Cronbach

Introdução

Um professor da faculdade quer examinar a confiabilidade de um teste de personalidade. Eles, portanto, têm uma amostra de N = 90 alunos preenchê-lo. Os dados assim coletados estão em big-5.sav, parcialmente mostrado abaixo.

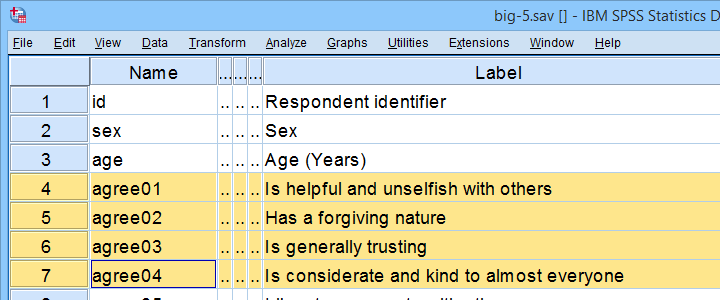
conforme sugerido pelos nomes das variáveis, nosso teste tenta medir os traços de personalidade” big 5″. Para outros arquivos de dados, uma análise fatorial é frequentemente usada para descobrir quais variáveis medem quais subescalas.

de qualquer maneira. Nossa principal questão de pesquisa é:quais são as confiabilidades para essas 5 subescalesas indicadas pelo Alfa de Cronbach? Mas primeiro: Qual é o alfa de Cronbach de qualquer maneira?

definição Alfa – rápida de Cronbach

alfa de Cronbach’s é a medida em que a soma sobre 2(+)
variáveis mede um único traço subjacente.Mais precisamente, o alfa de Cronbach é a proporção de variância de tal pontuação de soma que pode ser explicada por uma única característica. Ou seja, é até que ponto uma pontuação de soma mede algo de forma confiável e (portanto) até que ponto um conjunto de itens mede consistentemente “a mesma coisa”.

o alfa de Cronbach é, portanto, conhecido como uma medida de confiabilidade ou consistência interna. As regras mais comuns para isso são que

• alfa de Cronbach ≥ 0,80 é bom e
• alfa de Cronbach ≈ 0,70 pode ou não ser apenas aceitável.

SPSS Reliability Dialogs

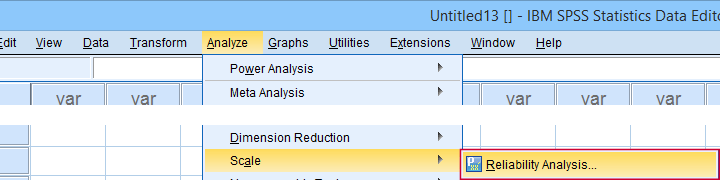
no SPSS, obtemos o alfa de Cronbach de Analyze Scale Reliability Analysis… como mostrado abaixo.

para analisar a primeira subescala, agreeableness, preenchemos os diálogos conforme mostrado abaixo.

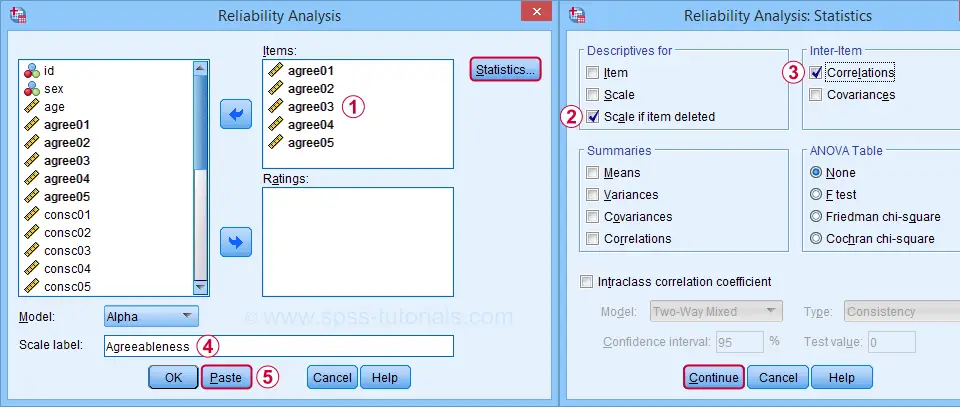
clicar em Colar resulta na sintaxe abaixo. Vamos lá.

saída Alfa de SPSS Cronbach I

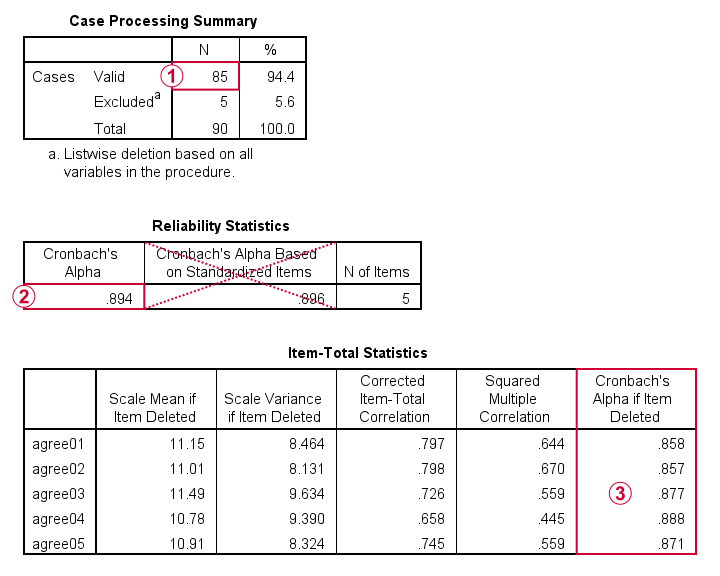
para confiabilidade, o SPSS oferece apenas exclusão listwise de valores ausentes: todos os resultados são baseados apenas em n = 85 casos com zero valores ausentes em nossas 5 variáveis de análise ou “itens”.
alfa de Cronbach = 0,894. Você geralmente pode ignorar o Alfa de Cronbach com base em itens padronizados: padronizar variáveis em escores z antes da Pontuação da escala de computação raramente é feito.
finalmente, excluir uma variável de uma escala (sub)pode aumentar o Alfa de Cronbach. Esse não é o caso nesta tabela: para cada item, o Alfa de Cronbach se o Item excluído for menor que o α = 0,894 com base em todos os 5 itens.

agora vamos executar exatamente a mesma análise para a nossa segunda subescala, conscienciosidade. Isso resulta na sintaxe abaixo.

aumente o Alfa de Cronbach removendo os itens

para a subescala de conscienciosidade, o alfa de Cronbach = 0,658, o que é muito ruim. No entanto, observe que o Alfa de Cronbach Se item excluído = 0,726 para consc02 e consc04.

uma vez que a remoção de qualquer item deve resultar em α ≈ 0,726, não temos certeza de qual deve ser removido primeiro. Duas maneiras de descobrir são

• aumentando as casas decimais ou (melhor)
• classificando a tabela por sua última coluna.

como você provavelmente viu, já fizemos os dois com os seguintes comandos de modificação de saída:

verifica-se que a remoção de consc04 aumenta alfa um pouco mais do que consc02. A maneira preferida de fazer isso é simplesmente copiar e colar o comando de confiabilidade anterior, remover o consc04 dele e executá-lo novamente.

depois de fazer isso, alfa de Cronbach = 0,724. Não é exatamente o previsto 0,726 porque a remoção do consc04 aumenta o tamanho da amostra para n = 84. Observe que podemos aumentar α ainda mais para 0,814 removendo consc02 também. A sintaxe abaixo faz exatamente isso.

observe que o alfa de Cronbach = 0,814 se calcularmos nossa subescala de conscienciosidade como a soma ou média acima de consc01, consc03 e consc05. Como tudo bem, terminamos com esta subescala.

vamos prosseguir com a próxima subescala: extroversão. Fazemos isso executando exatamente a mesma análise em extra01 para extra05, o que resulta na sintaxe abaixo.

o Alfa de Cronbach é negativo

como mostrado abaixo, o alfa de Cronbach = -0,663 para a subescala de extroversão. Isso implica que algumas correlações entre os itens são negativas (segunda tabela, abaixo).

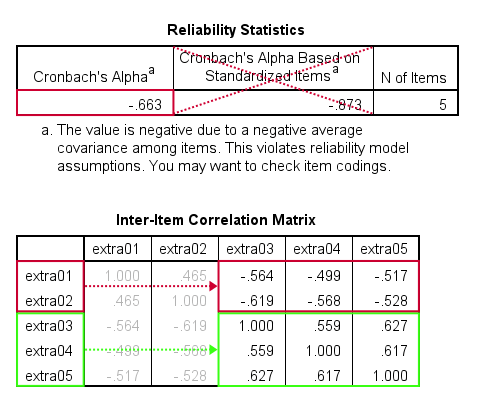
todos os itens de extroversão são codificados da mesma forma: eles têm rótulos de valor idênticos, então esse não é o problema. O problema é que alguns itens medem o oposto dos outros itens, conforme mostrado abaixo.

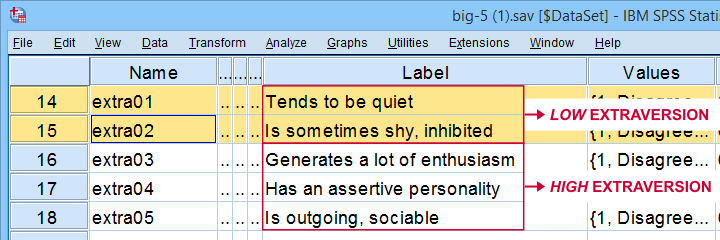
a solução é simplesmente reverter o código desses “itens negativos”: RECODIFICAMOS esses 2 itens e ajustamos seus rótulos de valor/variável com a sintaxe abaixo.

Executar novamente a mesma análise de confiabilidade exata da anterior agora resulta no alfa de Cronbach = 0,857 para a subescala de extroversão.

então vamos prosseguir com a subescala neuroticismo. A sintaxe abaixo executa nossa análise de confiabilidade padrão no neur01 para neur05.

existem poucos casos (N = 0) para a análise

observe que nosso último comando não resulta em nenhuma tabela útil. Nós só recebemos o aviso mostrado abaixo.

As 3 causas mais prováveis para este problema são que

• uma ou mais variáveis contém apenas os valores em falta;
• um FILTRO incorreto filtra todos os casos em que os dados;
• valores em falta são espalhados através de inúmeras análise de variáveis.

uma maneira muito rápida de descobrir é executar um comando descritivos mínimo como indescritivos neur01 para neur05.Ao fazer isso, aprendemos que cada variável tem n ≥ 67, mas n válido (listwise) = 0.

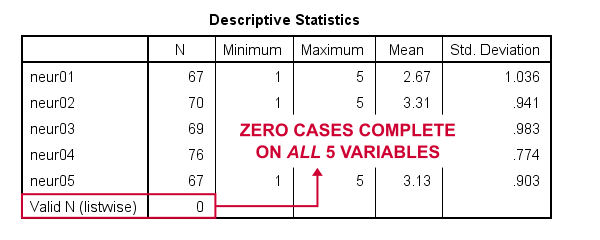
portanto, o que realmente queremos aqui é usar a exclusão em pares de valores ausentes. Por alguma razão Idiota, isso não está incluído no SPSS. No entanto, fazê-lo manualmente não é tão difícil quanto parece.

Alfa de Cronbach com Par de Exclusão de Valores em Falta

vamos começar com a fórmula para o alfa de Cronbach, que é o

$$Cronbach\;\alpha = \frac{k^2 \overline{S_{xy}}}{\Sigma S^2_x + 2 \Sigma S_{xy}}$$

onde

• \(k\) indica o número de itens;
• \(S_{xy}\) denota a covariância entre cada par de itens diferentes;
• \(S^2_x\) denota a variância da amostra para cada item.

observe que uma matriz de covariância em pares contém todas as estatísticas usadas por esta fórmula. É facilmente obtido através da sintaxe de regressão abaixo:

em seguida, copiamos o resultado para este Googlesheet. Finalmente, um punhado de fórmulas muito simples nos diz Que α = 0,889.

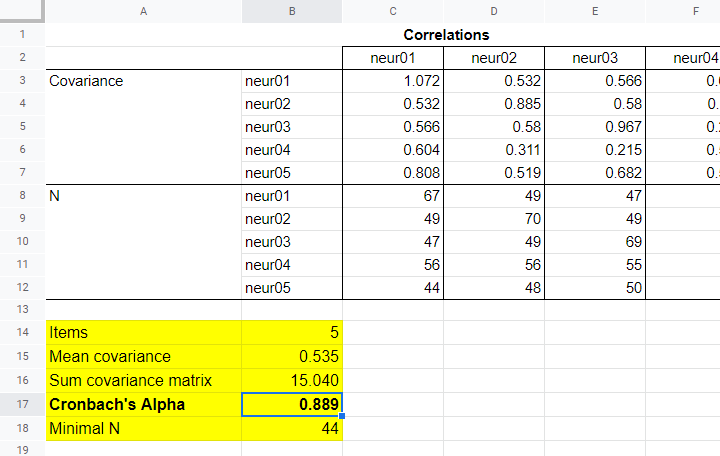
agora, qual tamanho de amostra devemos relatar para esta subescala? Proponho que você siga as convenções para regressão em pares aqui e relate o menor N em pares, o que resulta em N = 44 para esta análise. Novamente, observe que a fórmula para encontrar esse mínimo em um bloco de células é totalmente simples.

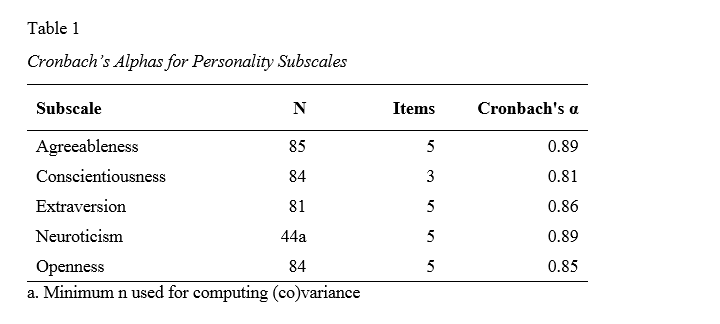
apa relatando Alfa de Cronbach

a tabela abaixo mostra como relatar alfa de Cronbach no estilo APA para todas as subescalas.