• Articles
• admin

• Alfa Cronbacha – szybka definicja
• SPSS wyjście Alfa Cronbacha
• zwiększ Alfę Cronbacha, usuwając elementy
• Alfa Cronbacha jest ujemna
• są też kilka przypadków (N = 0) do analizy
• raport APA alfa cronbacha

wprowadzenie

wydział psychologii chce zbadać wiarygodność testu osobowości. W związku z tym mają próbkę N = 90 uczniów wypełnić go. Zebrane w ten sposób dane są w big-5.sav, częściowo pokazany poniżej.

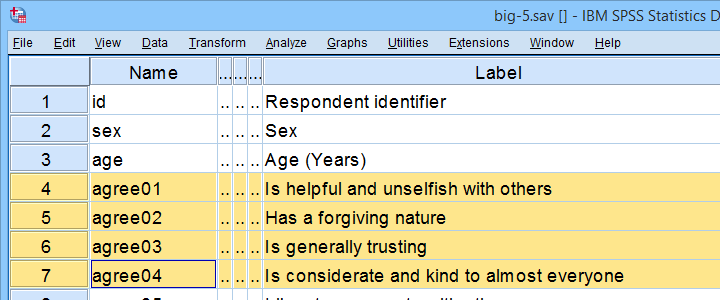
jak sugerują nazwy zmiennych, nasz test próbuje zmierzyć cechy osobowości „wielkiej piątki”. W przypadku innych plików danych często stosuje się analizę czynnikową, aby dowiedzieć się, które zmienne mierzą które podskale.

Nasze główne pytanie badawcze brzmi: Jakie są niezawodności dla tych 5 podskali wskazywanych przez Alfę cronbacha? Ale po pierwsze: co to jest Alfa cronbacha?

Alfa Cronbacha – szybka definicja

Alfa cronbacha to zakres, w jakim suma ponad 2 (+)
zmiennych mierzy jedną podstawową cechę.Dokładniej, Alfa cronbacha jest proporcją wariancji takiego wyniku sumy, która może być rozliczona przez pojedynczą cechę. Oznacza to, że jest to stopień, w jakim wynik sumy wiarygodnie mierzy coś, a tym samym stopień, w jakim zbiór elementów konsekwentnie mierzy „to samo”.

Alfa cronbacha jest zatem znana jako miara niezawodności lub spójności wewnętrznej. Najczęstsze zasady są takie, że

• Alfa cronbacha ≥ 0,80 jest dobra, a
• alfa cronbacha ≈ 0,70 może, ale nie musi być po prostu akceptowalna.

okna dialogowe niezawodności SPSS

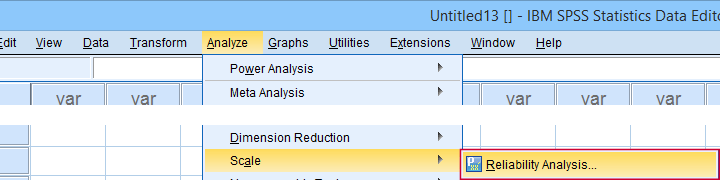
w SPSS otrzymujemy Alfę Cronbacha z analizy Skala Analiza niezawodności… jak pokazano poniżej.

aby przeanalizować pierwszą podskalę, wypełniamy okna dialogowe, jak pokazano poniżej.

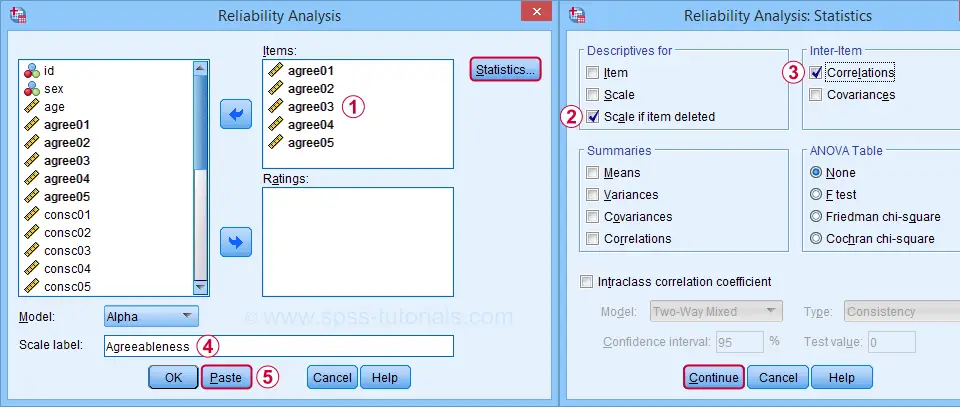
kliknięcie Wklej powoduje wyświetlenie poniższej składni. Sprawdźmy to.

wyjście SPSS Cronbachs Alpha i

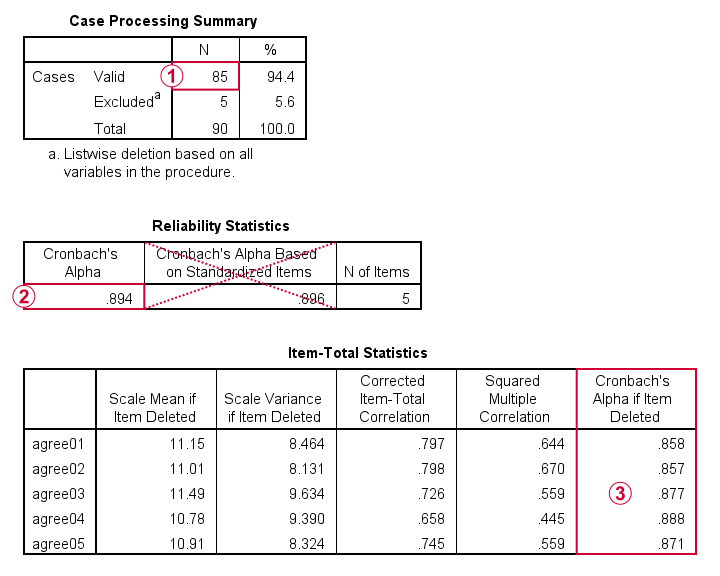
aby zapewnić niezawodność, SPSS oferuje tylko wykluczenie brakujących wartości listwise: wszystkie wyniki są oparte tylko na N = 85 przypadkach mających zero brakujących wartości na naszych 5 zmiennych analitycznych lub „items”.
Zazwyczaj można zignorować Alfę Cronbacha w oparciu o znormalizowane Elementy: standaryzacja zmiennych w z-scores przed obliczeniem scale scores jest rzadko – jeśli w ogóle-wykonywana.
wreszcie wykluczenie zmiennej ze skali (sub)może zwiększyć Alfa Cronbacha. Tak nie jest w tej tabeli: dla każdej pozycji Alfa Cronbacha, jeśli usunięta pozycja jest niższa niż α = 0,894 na podstawie wszystkich 5 pozycji.

przeprowadzimy teraz dokładnie tę samą analizę dla naszej drugiej podskali, sumienności. Powoduje to poniższą składnię.

zwiększ Alfę Cronbacha usuwając elementy

dla sumienności, Alfa cronbacha = 0,658, co jest dość słabe. Należy jednak pamiętać, że usunięta pozycja Alpha if Cronbacha = 0,726 zarówno dla consc02, jak i consc04.

ponieważ usunięcie dowolnego elementu powinno spowodować α ≈ 0.726, nie jesteśmy pewni, który powinien zostać usunięty jako pierwszy. Dwa sposoby, aby dowiedzieć się, to

• zwiększenie miejsc po przecinku lub (lepiej)
• sortowanie tabeli według ostatniej kolumny.

jak zapewne widzieliście, zrobiliśmy już oba z następującymi wyjściowymi poleceniami modyfikacji:

okazuje się, że usunięcie consc04 zwiększa alpha nieco więcej niż consc02. Preferowanym sposobem jest skopiowanie i wklejenie poprzedniego polecenia RELIABILITY, usunięcie z niego consc04 i ponowne uruchomienie.

po wykonaniu tej czynności Alfa cronbacha = 0,724. Nie jest to dokładnie przewidywane 0,726, ponieważ usunięcie consc04 zwiększa rozmiar próbki do N = 84 . Zauważ, że możemy zwiększyć α jeszcze dalej do 0,814, usuwając również consc02. Poniższa składnia właśnie to robi.

zauważ, że alfa Cronbacha = 0,814 jeśli obliczymy naszą sumienność jako sumę lub średnią nad consc01, consc03 i consc05. Skoro to jest w porządku, skończyliśmy z tą podskalą.

przejdźmy do następnego podskala: extraversion. Robimy to, wykonując dokładnie tę samą analizę na extra01 do extra05, co skutkuje poniższą składnią.

Alfa Cronbacha jest ujemna

jak pokazano poniżej, Alfa cronbacha = -0,663 dla podskali ekstrawersji. Oznacza to, że niektóre korelacje między pozycjami są ujemne (druga tabela, poniżej).

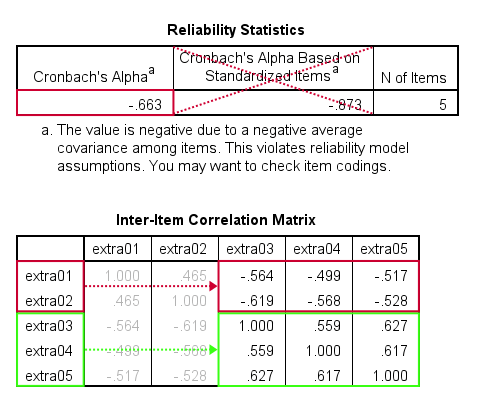
wszystkie elementy ekstrawersji są kodowane podobnie: mają identyczne etykiety wartości, więc to nie problem. Problem polega na tym, że niektóre elementy mierzą przeciwieństwo innych elementów, jak pokazano poniżej.

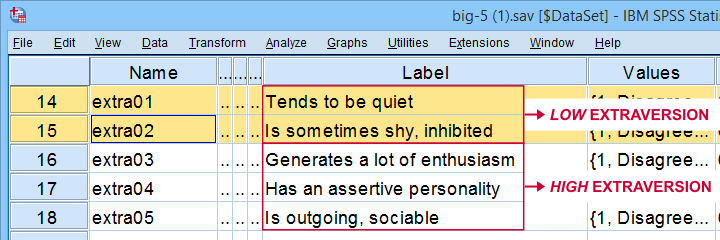
rozwiązaniem jest po prostu odwrócenie kodu takich „negatywnych elementów”: PRZEKODUJEMY te 2 elementy i dostosowujemy ich etykiety wartości/zmiennej za pomocą poniższej składni.

ponowne uruchomienie dokładnie tej samej analizy niezawodności, co poprzednio, daje teraz alpha cronbacha = 0,857 dla podskali ekstrawersji.

przejdźmy więc do podskali neurotyczności. Poniższa składnia uruchamia naszą domyślną analizę niezawodności od neu01 do neu05.

jest zbyt mało przypadków (N = 0) do analizy

zauważ, że nasze ostatnie polecenie nie daje żadnych użytecznych tabel. Dostajemy tylko Ostrzeżenie pokazane poniżej.

3 najbardziej prawdopodobnymi przyczynami tego problemu są to, że

• jedna lub więcej zmiennych zawiera tylko brakujące wartości;
• nieprawidłowy filtr filtruje wszystkie przypadki w danych;
• brakujące wartości są rozproszone po wielu zmiennych analizy.

bardzo szybkim sposobem na sprawdzenie jest uruchomienie komendy minimal DESCRIPTIVES jako indescriptives neu01 do neu05.Robiąc to, dowiadujemy się, że każda zmienna ma N ≥ 67, ale ważne N (listwise) = 0.

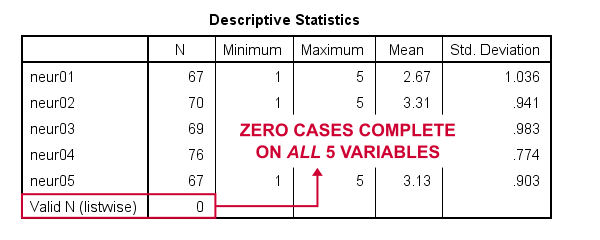
więc to, co naprawdę chcemy tutaj, to użycie parowego wykluczenia brakujących wartości. Z jakiegoś głupiego powodu, to nie jest zawarte w SPSS. Jednak robienie tego ręcznie nie jest tak trudne, jak się wydaje.

Alfa Cronbacha z wykluczeniem par brakujących wartości

zaczniemy od wzoru na alfa Cronbacha, który wynosi

$$\;\alpha = \ frac{k^2 \overline{S_{XY}}} {\Sigma s^2_x + 2 \ Sigma s_{xy}}$$

gdzie

• \(k\) oznacza liczbę elementów;
• \(s_{XY}\) oznacza kowariancję między każdą parą różnych elementów;
• \(s^2_x\) oznacza wariancję próbki dla każdego elementu.

zauważ, że macierz kowariancji pary zawiera Wszystkie Statystyki używane przez ten wzór. Można go łatwo uzyskać za pomocą poniższej składni regresji:

następnie kopiujemy wynik do tego Googlesheeta. Na koniec garść bardzo prostych wzorów mówi nam, że α = 0,889.

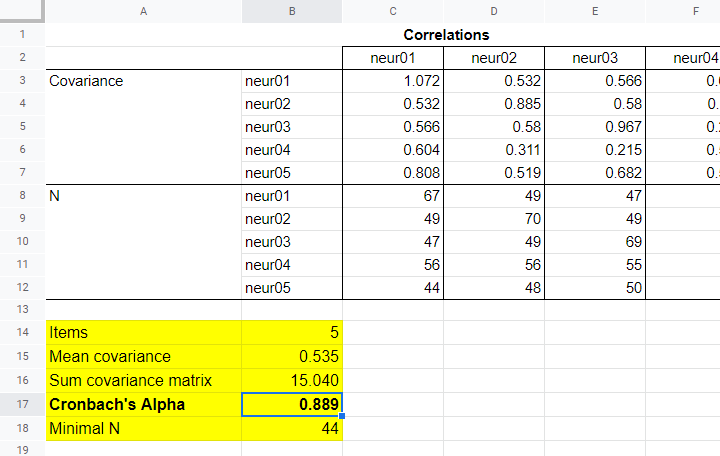
teraz, jaki rozmiar próbki powinniśmy zgłosić dla tej podskali? Proponuję postępować zgodnie z konwencjami regresji parowej i zgłosić najmniejsze pary n, co daje N = 44 do tej analizy. Ponownie, zauważ, że wzór na znalezienie tego minimum nad blokiem komórek jest całkowicie prosty.

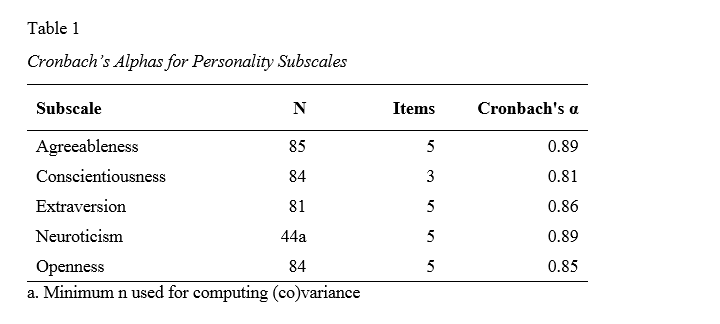
Apa raportowanie Alfa Cronbacha

poniższa tabela pokazuje, jak zgłosić Alfa Cronbacha w stylu APA dla wszystkich podskali.