• Articles
• admin

• Cronbach ’s Alpha – Quick Definition
• SPSS Cronbach’ s Alpha Output
• verhoog Cronbach ’s Alpha door het verwijderen van Items
• Cronbach’ s Alpha is negatief
• er zijn te weinig gevallen (n = 0) voor de analyse
• APA rapportage Cronbachs Alpha

Inleiding

een faculteit psychologie wil de betrouwbaarheid van een persoonlijkheidstest onderzoeken. Ze hebben daarom een steekproef van n = 90 studenten invullen. De aldus verzamelde gegevens zijn in big-5.sav, gedeeltelijk hieronder weergegeven.

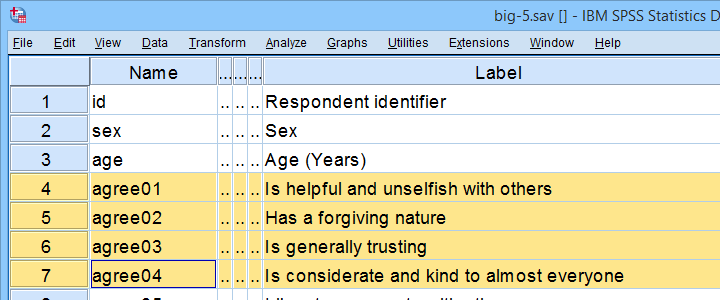
zoals gesuggereerd door de namen van de variabelen, probeert onze test de “big 5” persoonlijkheidskenmerken te meten. Voor andere gegevensbestanden wordt vaak een factoranalyse gebruikt om uit te vinden welke variabelen welke subschalen meten.

in ieder geval. Onze belangrijkste onderzoeksvraag is: wat zijn de betrouwbaarheid van deze 5 subscalesas aangegeven door Cronbach ‘ s alpha? Maar ten eerste: wat is Cronbach ‘ s alpha eigenlijk?

Cronbach ‘ s Alpha – Quick definitie

cronbach’s alpha is de mate waarin de som meer dan 2(+)
variabelen een enkele onderliggende eigenschap meet.Cronbachs alfa is de variantieverhouding van zo ‘ n somscore die kan worden verklaard door een enkele eigenschap. Dat wil zeggen, het is de mate waarin een somscore iets betrouwbaar meet en (dus) de mate waarin een verzameling items consequent “hetzelfde”meet.

Cronbach ‘ s alpha staat daarom bekend als een maatstaf voor betrouwbaarheid of interne consistentie. De meest voorkomende vuistregels zijn dat

• Cronbach ’s Alfa ≥ 0,80 goed is en
• Cronbach’ s Alfa ≈ 0,70 al dan niet aanvaardbaar is.

SPSS Betrouwbaarheidsdialogen

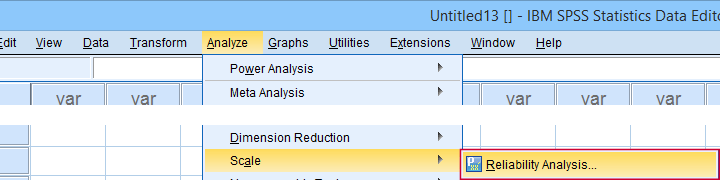
in SPSS krijgen we de alpha van Cronbach uit analyse Schaal betrouwbaarheidsanalyse… zoals hieronder getoond.

voor het analyseren van de eerste subschaal, agreeableness, vullen we de onderstaande dialogen in.

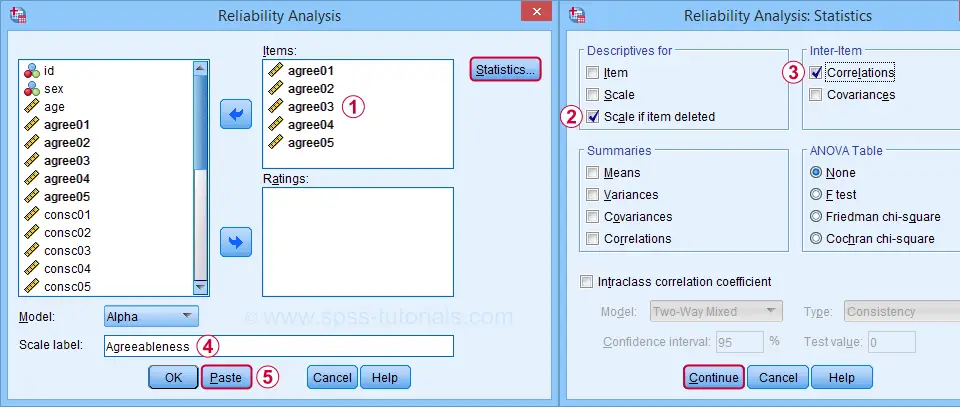
klikken op Plakken resulteert in onderstaande syntaxis. Laten we het natrekken.

SPSS Cronbach ‘ s Alpha Output i

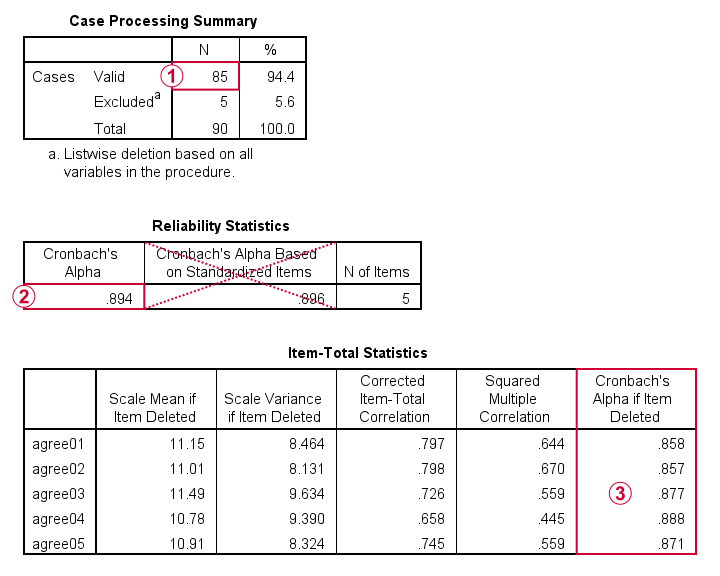
voor betrouwbaarheid biedt SPSS alleen listwise uitsluiting van ontbrekende waarden: alle resultaten zijn alleen gebaseerd op n = 85 gevallen met nul ontbrekende waarden op onze 5 analyse variabelen of “items”.
Cronbach ‘ s alpha = 0,894. U kunt Cronbach ‘ s Alpha meestal negeren op basis van gestandaardiseerde Items: het standaardiseren van variabelen in z-scores voorafgaand aan het berekenen van scale scores wordt zelden of nooit gedaan.
ten slotte kan het uitsluiten van een variabele van een (sub)schaal Cronbach ‘ s Alfa verhogen. Dat is niet het geval in deze tabel: voor elk item, Cronbach ‘ s Alpha Als Item verwijderd is lager dan de α = 0,894 op basis van alle 5 items.

we zullen nu exact dezelfde analyse uitvoeren voor onze tweede subschaal, consciëntiousness. Dit resulteert in de syntaxis hieronder.

verhoog Cronbach ’s Alpha door Items

te verwijderen voor de subschaal consciëntiousness, Cronbach’ s alpha = 0,658, wat vrij slecht is. Merk echter op dat Cronbach ‘ s Alpha if Item verwijderd = 0,726 voor zowel consc02 en consc04.

omdat het verwijderen van een van beide items zou moeten resulteren in α ≈ 0,726, weten we niet zeker welke als eerste verwijderd moet worden. Twee manieren om erachter te komen zijn

• het verhogen van de decimalen of (beter)
• het sorteren van de tabel op de laatste kolom.

zoals u waarschijnlijk zag, hebben we beide al gedaan met de volgende uitvoer MODIFY commando’s:

het blijkt dat het verwijderen van consc04 de Alfa iets meer verhoogt dan consc02. De beste manier om dit te doen is om simpelweg het vorige BETROUWBAARHEIDSCOMMANDO te kopiëren-plakken, consc04 eruit te verwijderen en het opnieuw uit te voeren.

na dit te hebben gedaan, Cronbach ‘ s alpha = 0,724. Het is niet precies de voorspelde 0,726 omdat het verwijderen van consc04 de steekproefgrootte verhoogt tot n = 84. Merk op dat we α nog verder kunnen verhogen tot 0,814 door ook consc02 te verwijderen. De syntaxis hieronder doet precies dat.

merk op dat Cronbach ‘ s alpha = 0,814 als we onze consciëntiousness subschaal berekenen als de som of het gemiddelde over consc01, consc03 en consc05. Aangezien dat prima is, zijn we klaar met deze subschaal.

laten we doorgaan met de volgende subschaal: extraversion. We doen dit door het uitvoeren van exact dezelfde analyse op extra01 tot extra05, wat resulteert in de syntaxis hieronder.

Cronbach ’s Alpha is negatief

zoals hieronder getoond, Cronbach’ s alpha = -0,663 voor de extraversion subschaal. Dit houdt in dat sommige correlaties tussen items negatief zijn (tweede tabel, hieronder).

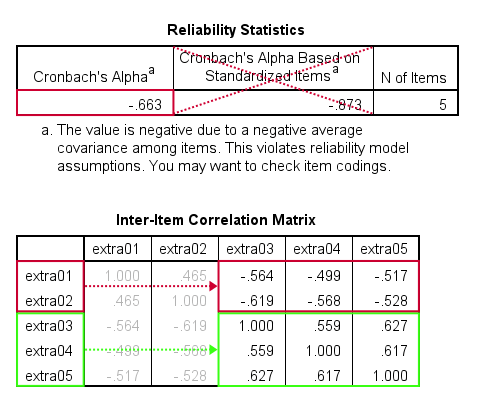
alle Extraversion-items worden op dezelfde manier gecodeerd: ze hebben identieke waarde-labels, dus dat is niet het probleem. Het probleem is dat sommige items meten het tegenovergestelde van de andere items zoals hieronder weergegeven.

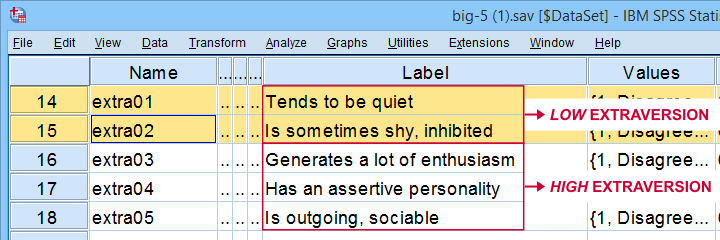
de oplossing is om dergelijke “negatieve items” simpelweg om te keren: we hercoderen deze 2 items en passen hun waarde/variabele labels aan met de syntaxis hieronder.

het opnieuw uitvoeren van exact dezelfde betrouwbaarheidsanalyse als de vorige resulteert nu in Cronbach ‘ s alpha = 0,857 voor de Extraversion subschaal.

dus laten we doorgaan met de subschaal neuroticisme. De syntaxis hieronder voert onze standaard betrouwbaarheids analyse uit op neur01 tot neur05.

er zijn te weinig gevallen (N = 0) voor de analyse

merk op dat ons laatste commando niet resulteert in bruikbare tabellen. We krijgen alleen de onderstaande waarschuwing.

de drie meest waarschijnlijke oorzaken voor dit probleem zijn dat

• één of meer variabelen alleen ontbrekende waarden bevat;
• een onjuist FILTER filtert alle gevallen uit de gegevens;
• ontbrekende waarden zijn verspreid over talrijke analysevariabelen.

een zeer snelle manier om erachter te komen is het uitvoeren van een minimal DESCRIPTIVES commando als indescriptives neur01 tot neur05.Als we dit doen, leren we dat elke variabele n ≥ 67 heeft maar geldig N ( listwise) = 0.

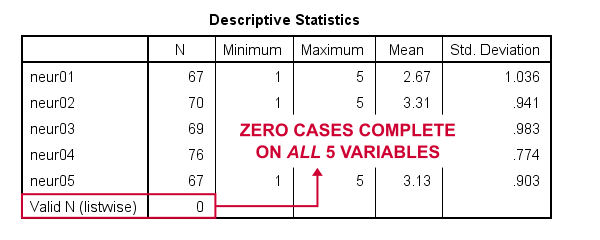
dus wat we hier echt willen, is het gebruik van paarsgewijze uitsluiting van ontbrekende waarden. Om een of andere domme reden, dat is niet opgenomen in SPSS. Echter, het handmatig doen is niet zo moeilijk als het lijkt.

cronbach ’s Alpha met Paarsgewijze Uitsluiting van Ontbrekende Waarden

We beginnen met de formule van cronbach’ s alpha, dat is

$$cronbach ‘ s\;\alpha = \frac{k^2 \overline{S_{xy}}}{\Sigma S^2_x + 2 \Sigma S_{xy}}$$

waar

• \(k\) geeft het aantal items;
• \(S_{xy}\) geeft de covariantie tussen elk paar van de verschillende items;
• \(S^2_x\) geeft de steekproefvariantie voor elk item.

merk op dat een paarsgewijze covariantiematrix alle statistieken bevat die door deze formule worden gebruikt. Het is gemakkelijk te verkrijgen via de onderstaande regressiesyntaxis:

vervolgens kopiëren we het resultaat naar dit Googlesheet. Tot slot, een handvol zeer eenvoudige formules vertellen ons dat α = 0,889.

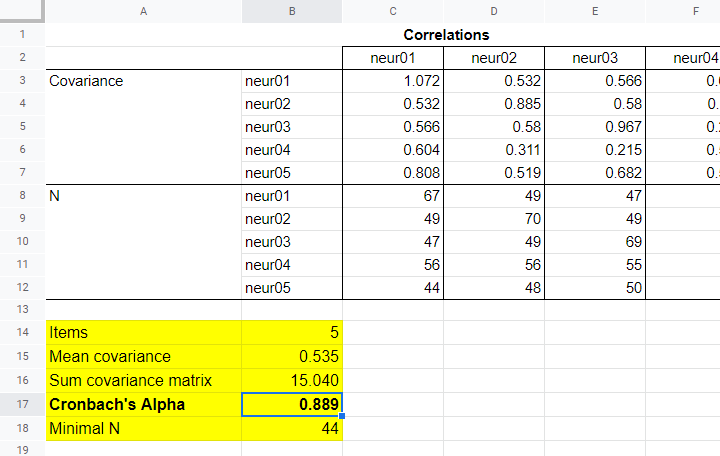
nu, welke steekproefgrootte moeten we rapporteren voor deze subschaal? Ik stel voor dat u hier de conventies voor paarsgewijze regressie volgt en de kleinste paarsgewijze n rapporteert die resulteert in n = 44 voor deze analyse. Merk nogmaals op dat de formule voor het vinden van dit minimum over een blok cellen volkomen eenvoudig is.

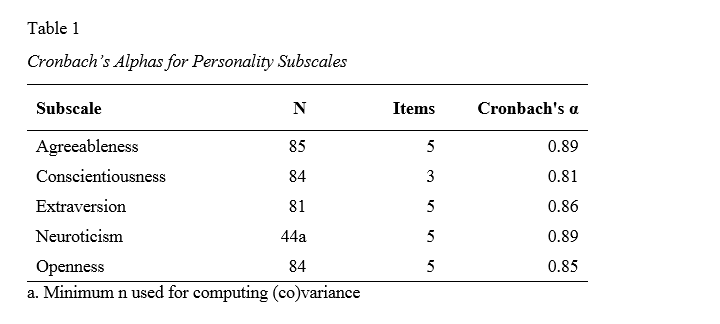
APA rapportage van Cronbach ’s Alpha

de tabel hieronder laat zien hoe Cronbach’ s alpha in APA-stijl voor alle subschalen moet worden gerapporteerd.