• Articles
• admin

• Cronbachのアルファ-クイック定義
• SPSS Cronbachのアルファ出力
• 項目を削除してCronbachのアルファを増分析のためのいくつかのケース（n=0）
• apa報告cronbachのアルファ

はじめに

心理学の教員は、人格テストの信頼性を調べたいと考えています。 したがって、彼らはN=90の学生のサンプルを記入しています。 このようにして収集されたデータはbig-5にあります。savは、部分的に以下に示す。SPSSサンプルデータファイルの

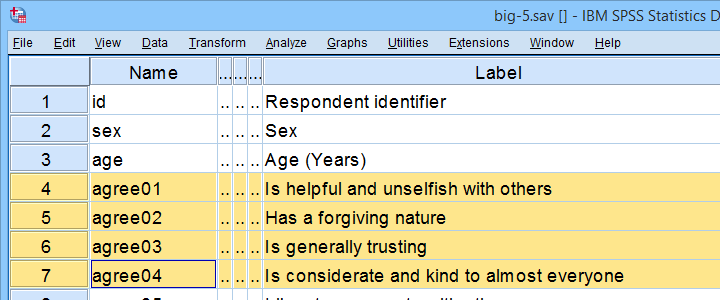
変数名で示唆されているように、私たちのテストは「big5」の性格特性を測定しようとします。 他のデータファイルの場合、因子分析は、どの変数がどの従属スケールを測定するかを調べるために使用されることがよくあります。

私たちの主な研究課題は、Cronbachのアルファによって示されるこれらの5つのサブスカリサスの信頼性は何ですか？ しかし、まず第一に：とにかくCronbachのアルファは何ですか？

Cronbachのアルファ-クイック定義

Cronbach’sのアルファは、2つの（+）
変数の合計が単一の基礎となる特性を測定する程度です。より正確には、Cronbachのアルファは、単一の特性によって説明できるそのような合計スコアの分散の割合です。 つまり、sumスコアが確実に何かを測定する程度であり、（したがって）一連の項目が一貫して”同じもの”を測定する程度です。したがって、

Cronbachのアルファは、信頼性または内部一貫性の尺度として知られています。 そのための最も一般的な経験則は、

• Cronbachのalpha≈0.80が良好であり、
• Cronbachのalpha≈0.70が許容される場合とそうでない場合があるということです。

SPSS信頼性ダイアログ

SPSSでは、AnalyzeScaleReliability AnalysisからCronbachのアルファを取得します。.. 以下に示すように。

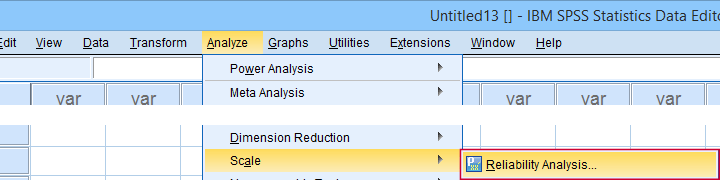
最初のサブスケールであるagreeablenessを分析するには、以下のようにダイアログを入力します。

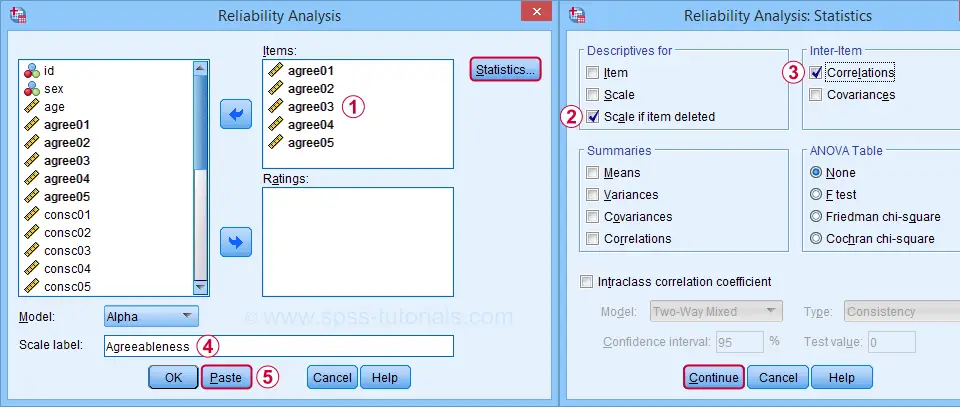
貼り付けをクリックすると、以下の構文が表示されます。 それを実行してみましょう。

SPSS Cronbachのアルファ出力I

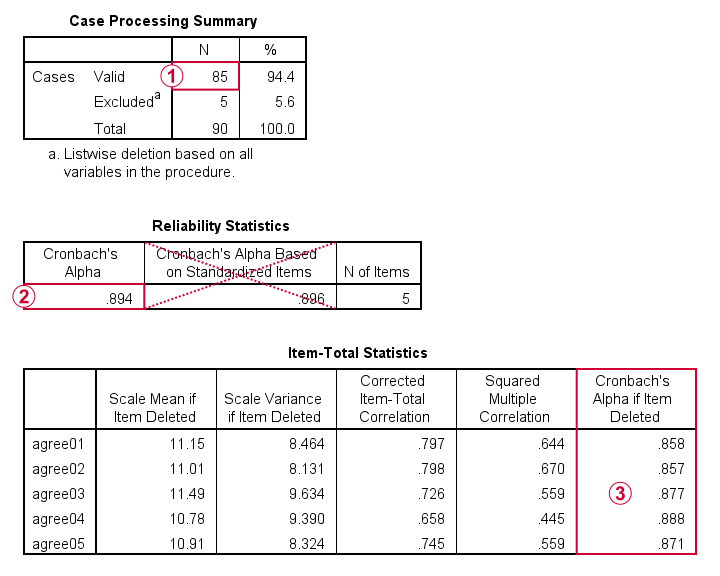
信頼性のために、SPSSは欠損値のリストごとの除外のみを提供します: すべての結果は、5つの分析変数または「アイテム」に欠損値がゼロのN=85ケースにのみ基づいています。
クロンバッハのアルファ=0.894。 スケールスコアを計算する前に変数をzスコアに標準化することはめったにありません。
最後に、（サブ）スケールから変数を除外すると、Cronbachのアルファが増加する可能性があります。 各アイテムについて、アイテムが削除された場合のCronbachのアルファは、5つのアイテムすべてに基づいてα=0.894よりも低くなります。

ここで、2番目のサブスケールであるconscientiousnessに対してまったく同じ分析を実行します。 これを行うと、以下の構文になります。

項目

を削除することにより、Cronbachのアルファを増加させます良心のサブスケールのために、Cronbachのアルファ=0.658、これはかなり悪いです。 ただし、cronbachのAlpha If Item Deleted=0.726は、consc02とconsc04の両方であることに注意してください。

いずれかのアイテムを削除するとα≤0.726になるため、どちらを最初に削除するかはわかりません。 見つける2つの方法は、小数点以下の桁数を増やすか（より良い）

テーブルを最後の列でソートすることです。

おそらく見たように、次の出力変更コマンドですでに両方を行いました。

consc04を削除すると、αがconsc02よりもわずかに増加することが判明しました。 これを行うための推奨される方法は、以前のRELIABILITYコマンドをコピーして貼り付け、そこからconsc04を削除して再実行することです。

その後、Cronbachのアルファ=0.724。 Consc04を削除するとサンプルサイズがN=84に増加するため、正確には予測された0.726ではありません。 Consc02も削除することでαをさらに0.814に増やすことができることに注意してください。 以下の構文はそれを行います。

良心の従属スケールをconsc01、consc03、consc05の合計または平均として計算すると、Cronbachのalpha=0.814であることに注意してください。 それは大丈夫なので、このサブスケールは終わりです。

次のサブスケール:extrversionに進みましょう。 これを行うには、extra01からextra05でまったく同じ分析を実行し、以下の構文になります。

Cronbachのアルファは負の

以下に示すように、cronbachのアルファ=-0.663extrversionのサブスケール。 これは、項目間のいくつかの相関が負であることを意味する（下の第二の表）。

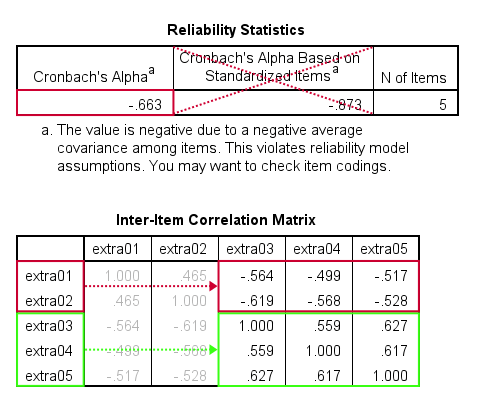
すべてのextrversion項目は同様にコード化されています。 問題は、以下に示すように、いくつかの項目が他の項目の反対を測定することです。

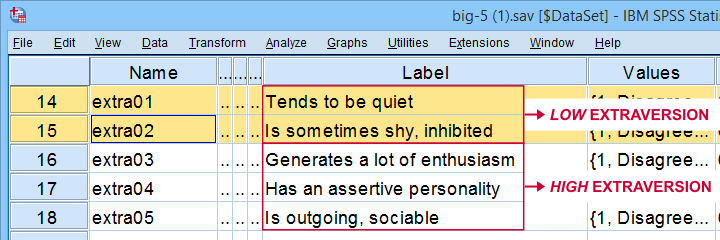
解決策は、単にそのような”負の項目”のコードを逆にすることです：これらの2つの項目を再コード化し、その値/変数ラベルを以下の構文で調整します。

前回とまったく同じ信頼性解析を再実行すると、extrversionのサブスケールに対してCronbachのalpha=0.857になります。

では、神経症のサブスケールを進めましょう。 以下の構文は、neur01からneur05までのデフォルトの信頼性分析を実行します。

分析にはケースが少なすぎます（N=0）

最後のコマンドでは有用なテーブルが得られないことに注意してください。 以下に示す警告のみが表示されます。

この問題の3つの最も可能性の高い原因は、

• 一つ以上の変数に欠損値のみが含まれていることです。
• 誤ったフィルターがデータ内のすべてのケースをフィルタリングします。
• 欠損値は多数の分析変数に散在しています。

見つけるための非常に簡単な方法は、indescriptives neur01からneur05として最小限の記述コマンドを実行することです。そうすると、各変数にはN≥67がありますが、有効なN（listwise）=0であることがわかります。

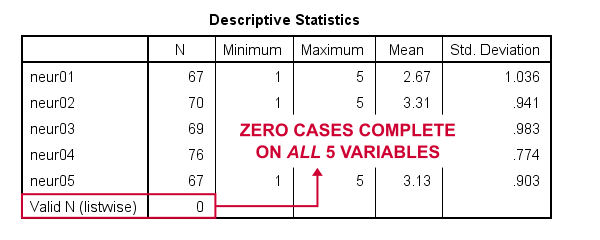
だから、ここで本当に欲しいのは、欠損値のペアワイズ除外を使用することです。 いくつかの愚かな理由で、それはSPSSに含まれていません。 しかし、それを手動で行うことはそれほど難しくありません。私たちは、

であるCronbachのアルファのための式から始めましょう

cr Cronbachの\;\alpha=\frac{k^2\overline{S_{xy}}}{\sigma S^2_x+2\sigma S_{xy}}=\frac{k^2\overline{S_{xy}}}{\sigma S^2_x+2\sigma S_{xy}}=\frac{k^2\overline{S_{xy}}{\sigma S^2_x+2\sigma S_{xy}}=\frac{k^2\overline{S_{xy}}{\sigma S^2_x+2\sigma S_{xy}}=\frac{k^2\overline{S_{xy}}{\sigma}}$$

どこで

• \(k\)はアイテムの数を表し、
• \(S_{xy}\)は異なるアイテムの各ペア間の共分散を表し、
• \(S^2_x\)は各アイテムのサンプル分散を表します。

ペアワイズ共分散行列には、この式で使用されるすべての統計が含まれていることに注意してください。 これは、以下の回帰構文を介して簡単に取得できます。

次に、結果をこのGooglesheetにコピーします。 最後に、非常に簡単な数式の一握りは、α=0.889ことを教えてくれます。

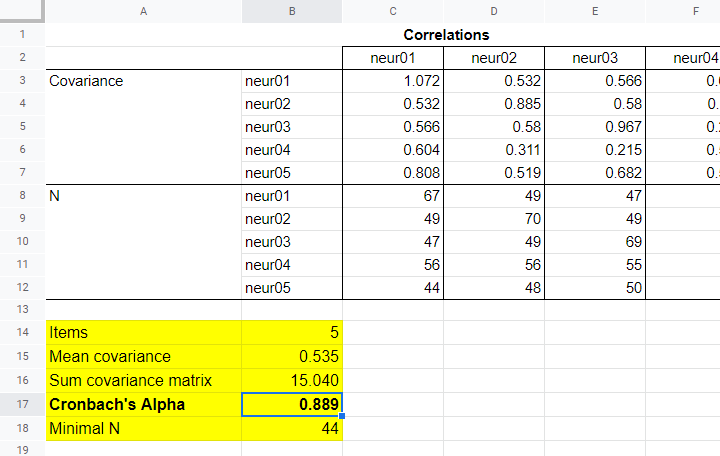
さて、このサブスケールに対してどのサンプルサイズを報告すべきですか？ ここでは、ペアワイズ回帰の規則に従い、この分析ではn=44の最小のペアワイズNを報告することを提案します。 繰り返しになりますが、セルのブロックでこの最小値を見つけるための式はまったく簡単です。

APAレポートCronbachのアルファ

以下の表は、すべてのサブスケールについてCRONBACHのアルファをAPAスタイルでレポートする方法を示しています。