• Articles
• admin

Hej ECI831,

der er situationer i vores daglige liv, når vi skal beregne procentdel i vores sind, og disse scenarier er ret almindelige. Hvornår var sidste gang vi talte med vores venner, kolleger eller studerende om procentdel? sandsynligvis i restauranter, afsked ting med venner eller mens du diskuterer med eleverne om deres karakterer, betaler husleje, pant disse virkelige situationer er almindelige, og hvad hvis vi kan gøre det hurtigere og i vores sind nemt. Vedisk matematik tilbyder en pæn løsning på disse problemer.

i min tidligere blog lærte vi divisionsmetode ,når divisoren er 9 og også Nikhilam formel,i dag i dette indlæg skal vi lære at finde procentdel af ethvert tal ved hjælp af vedisk matematik.

nedenstående billede er en simpel illustration af forskellen mellem sædvanlig metode og Vedisk metode

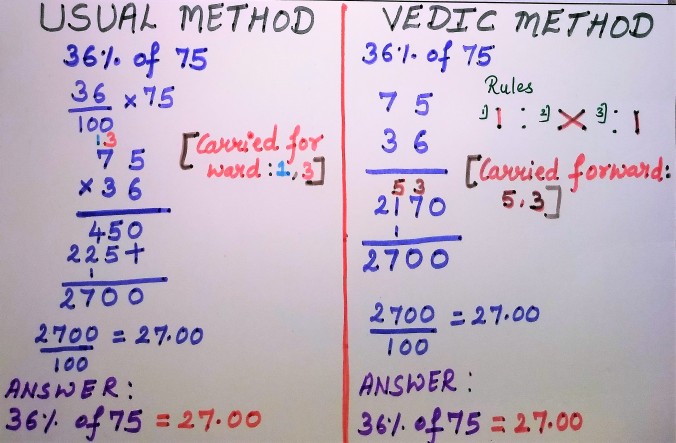
for at finde procentdelen skal vi anvende sutraen eller formlen, dvs .lodret og krydsvis multiplikation.som vi har lært i multiplikation metode .
ved at bruge ovenstående formel vil jeg løse nogle eksempler.
1) Lader os finde den procentdel af 36 liter 85
trin
i) Skriv de givne værdier i to rækker
3 6
8 5
ii) nu vil vi anvende teknikken til lodret og krydsvis multiplikation , overveje det 1.par ,hvor krydsmultiplikation ikke er mulig, vi løser det ved lodret multiplikation.
3 6
↓ (3×8=24)
8 5
24
iii) overvej 2 par, her er krydsmultiplikation mulig, så vi anvender den samme regel.
3 6
. Χ
8 5 (15 + 48=63)
6 (BÅRET FREM)
(24) 3
iv) Næste overveje det sidste par der kun er et par tilbage , så vil vi anvender vertikale multiplikation metode.
3 6
. ↓ (6×5=30)
8 5
6 3 (fremført)
(24) 3 0
V) Tilføj alle kolonnerne.
3 6
8 5
6 3 (fremført)
(24) 3 0
30 6 0 (Svar)
vi) Del svaret med 100 vi får det endelige svar
3060÷100=30.60
36⸓ af 85 = 30.60

2) lader os finde den procentdel af 52 liter 640
trin
i) Skriv de givne værdier i to rækker
0 5 2
6 4 0
ii) nu vil vi anvende teknikken til lodret og krydsvis multiplikation, overveje det 1.par,krydsmultiplikation er ikke mulig , vi løser det ved lodret multiplikation.
0 5 2
↓ (0×6=0)
6 4 0
0
iii) overvej 2 par, her er krydsmultiplikation mulig, så vi anvender den samme regel.
0 5 2
. Χ (0+30=30)
6 4 0
3 (BÅRET FREM)
0 for 0
iii)Overveje, 3 par, her på tværs af multiplikation er muligt,skal du gange ekstrem cifre af samarbejde på tværs af multiplikation og midterste ciffer ved den vertikale metode.
0 5 2
. Χ (0+12+20=32)
6 4 0
3 3 (BÅRET FREM)
0 0 2
iv) Næste overveje de sidste 2 par, på tværs af multiplikation er muligt, så vil vi anvende samme regel.
0 5 2
. Χ (0+8=8)
6 4 0
3 3 (BÅRET FREM)
0 0 2 8
v) Næste overveje det sidste par der kun er et par tilbage , så vil vi anvender vertikale multiplikation metode.
0 5 2
. ↓ (0×2=0)
6 4 0
3 3 (fremført)
0 0 2 8 0
vi) Tilføj alle kolonnerne
0 5 2
6 4 0
3 3 (fremført)
0 0 2 8 0
3 3 2 8 0 (Svar)

vi) Del svaret med 100 vi får det endelige svar
33280÷100=332.80
52⸓ af 640 = 332.80