hur man kör Monte Carlo-simuleringar i Excel
så du vill köra Monte Carlo-simuleringar i Excel, men ditt projekt är inte tillräckligt stort eller du gör inte den här typen av probabilistisk analys tillräckligt för att motivera att köpa ett dyrt tillägg. Du har kommit till rätt ställe. Excels inbyggda funktionalitet möjliggör stokastisk modellering, inklusive att köra så många simuleringar som datorns processorkraft kommer att stödja, och det här korta inlägget med videohandledning leder dig genom installationen och processen att köra Monte Carlo-simuleringar i Excel utan några tillägg som behövs.
probabilistisk analys från ett Fastighetsperspektiv
detta är en kommersiell fastighetsblogg, och därför ser denna handledning på stokastisk modellering ur en fastighetsproffs perspektiv. Den stora majoriteten av de tekniker som visas i detta inlägg kommer dock att fungera över discipliner.
jag noterar också att flera av de begrepp som visas här anpassade Jag från Keith Chin-Kee Leungs excellente examensarbete om ämnet: Beyond DCF Analysis in Real Estate Financial Modeling: Probabilistic Evaluation of Real Estate Ventures.

Monte Carlo simuleringar för fastigheter-Excel Nerd nivå: 1,000,000
vad detta är handledning är inte
detta inlägg är inte en kurs på sannolikhetsanalys. Som sådan förutsätter det att du har en grundläggande förståelse för Sannolikhet, statistik, Excel och vet vad en Monte Carlo-simulering är. Om du vill få en uppdatering om sannolikhet eller statistik i allmänhet rekommenderar jag att du tar en kurs i ämnet. Här är en gratis MOOC (massive open Online course) som erbjuds av Duke:
- introduktion till Sannolikhet och Data
scenariot – En lägenhetsavtal
innan du kör dina simuleringar behöver du ett scenario för att modellera. I det här fallet kommer vi att köra ett grundläggande diskonterat kassaflöde på en hypotetisk lägenhetsbyggnad för att bestämma hur mycket vi skulle vara villiga att betala för fastigheten idag. Här är vad vi vet:
- ämnet egendom har 10 enheter
- ämnet egendom avgifter $1000 / månad för varje enhet; hyrorna växer med 3% förra året
- det finns en enhet ledig, och för enkelhetens skull antar vi att det alltid kommer att finnas en enhet ledig
- kostnaderna är $3,000 per månad; kostnaderna växer med 2% förra året
- jämförbara fastigheter säljer för en 5.5% – 6.0% cap rate idag, men cap priser förväntas växa med cirka 5 punkter per år under de kommande åren (exit cap rate mellan 5.75% och 6.25%)
- planerar att hålla fastigheten i fem år
- rikta en 8% olevererad avkastning
ställa in modellen
därefter ställer jag in min Excel-modell som förberedelse för att köra simuleringarna (du kan ladda ner Excel-arbetsboken som används i den här handledningen i slutet av det här inlägget).
- i kolumn B och D faller jag i mina basantaganden
- Cell G2 jag märker ”DCF-värde”
- i rad 14, med början i cell F14 till K14, lägger jag till en periodrubrik med sex perioder inklusive en period noll
- Cell E15 jag märker ”hyra”
- Cell E16 i etikett ”expense”
- Cell E17 i etikett ”netto rörelseresultat”
- Cell E18 i etikett ”restvärde”
- cell L17 i etikett ”Exit Cap”
- cell E19 i lable ”nettokassaflöde”
- Cell D14 i Etikett ”tillväxttakt”
- i cell G15 skriver jag formeln: = 9*12 * $D$4 * (1 + $D15)^(G14-1) vilket betyder nio enheter (10 enheter mindre en ledig enhet), gånger 12 månader, gånger $d$4 ($1000 hyra/enhet/månad), gånger ett plus $D15 (den sannolika tillväxttakten beräknad i cell D15), upp till perioden (G15) minus en (jag subtraherar en eftersom vi inte vill hyra att växa i år ett). Eftersom de korrekta absoluta cellreferenserna har skapats (t.ex. $d$4 och $D15) kan jag sedan kopiera formeln rätt till cell K15.
- jag följer en liknande process för utgifter, med formeln: =$D$7*12*(1+$D16)^(G14-1) i cell G16 och kopierar sedan den formeln ut till cell K16.
- i cellerna G17 till K17 subtraherar jag kostnader från hyran (t.ex. i G17 skriver jag =G15-G16) för att komma fram till ett rörelseresultat för varje år.
- i cell K18 skriver jag formeln: =K17 / L18 vilket innebär att dividera år fem netto rörelseresultat med den sannolika exit cap rate (L18).
- i cellerna G19 till K19 lägger jag till nettokassaflödena för varje år: rörelseresultat netto i år ett till fyra och rörelseresultat netto plus restvärde år fem.
- slutligen beräknar jag i cell G3 nuvärdet av kassaflödesströmmen i rad 19 diskonterad tillbaka vid 8% (målfri avkastning) med formeln: =NPV(D12,G19:K19).
med DCF-inställningen kan jag nu gå vidare för att lägga till Sannolikhet för mina antaganden.
lägga Sannolikhet med hjälp av RANDBETWEEN () funktion
i vårt scenario ovan, Vi har ett par antaganden som är osäkra, och därför skulle vara bra kandidater för att lägga variabilitet till. Först måste vi välja en distributionstyp för vår Sannolikhet.
vi har ett antal alternativ, de två vanligaste är enhetlig fördelning (konstant Sannolikhet där alla resultat är lika troliga) och normalfördelning (tänk bell curve Sannolikhet där det resulterande värdet sannolikt kommer att vara närmare medelvärdet). För enkelhetens skull väljer vi en enhetlig fördelning.
- i cell D15 lägger jag till enhetlig variation i hyrestillväxten med formeln: =$D$5*RANDBETWEEN(-500,2000)/1000, vilket innebär att ta 3% (förra årets hyrestillväxt från cell $D$5) och multipla det med ett slumpmässigt tal mellan -0.5 och 2.0 (RANDBETWEEN (-50,200) / 100) så att den resulterande hyrestillväxten faller slumpmässigt mellan -1.5% och 6.0%.
- i cell D16 lägger jag till enhetlig variation i kostnadstillväxthastigheten med en liknande formel: =$D$8*RANDBETWEEN(-500,2000)/1000, bara i det här fallet tar jag förra årets kostnadstillväxthastighet (2% från cell $d$8) och multiplicerar den med ett slumpmässigt tal mellan -0,5 och 2,0 (RANDBETWEEN(-50,200)/100) så att den resulterande kostnadstillväxten faller slumpmässigt mellan -1.0% och 4.0%.
- slutligen, i Cell L18, lägger jag till enhetlig variation i utgångshastigheten med formeln: =D10*RANDBETWEEN(958.3,1041.7)/1000, vilket innebär att ta 6% (genomsnittet mellan 5.75% och 6.25% förväntat intervall för exit cap-priser i år fem) och multipla det med ett slumpmässigt tal mellan 0.9583 och 1.0417 (RANDBETWEEN(958.3,1041.7)/1000) så att den resulterande exit cap-hastigheten faller slumpmässigt mellan 5.75% och 6, 25%.
du kommer att se nu när du trycker på F9, att hyrestillväxten, kostnadstillväxten och utgångshastighetsvärdena ändras slumpmässigt, vilket resulterar i en slumpmässig förändring i kassaflödena och det totala diskonterade kassaflödesvärdet.
kör Monte Carlo-simuleringar med hjälp av datatabeller
med sannolikhet som läggs till i din modell kan du börja köra dina Monte Carlo-simuleringar. Denna process innebär att bygga en datatabell, kopplad till ditt DCF-värde (G3) så att varje simulering registrerar det resulterande DCF-värdet från den simuleringen.
så här kör vi Monte Carlo-simuleringarna med hjälp av Datatabellfunktionen i Excel:
- Cell B27 jag märker ”simulering #”
- jag länkar Cell C27 till DCF-värdet (=G3)
- jag numrerar celler B28 till B1027 från 1 till 1000. För att göra detta satte jag först cell B28 till 1. Jag anger sedan formeln = B28 + 1 i cell B29. Slutligen kopierar jag formeln i B29 ner till cell B1027.
- med simuleringarna numrerade och cell C27 kopplade till DCF-värdet väljer jag celler B27 till C1027 och klickar på funktionen ’datatabell’ (Data>vad-om-analys>Datatabell).
- jag lämnar rutan ’Row input cell:’ Tom och klickar på rutan’ Column input cell’. Jag väljer en tom cell i kalkylbladet (vilken cell spelar ingen roll så länge det är en cell som alltid är tom), tryck på enter och sedan ’OK’.
- datatabellen uppdateras med 1000 iterationer av vår simulering och voila du har kört en Monte Carlo-simulering i Excel med hjälp av datatabellen.
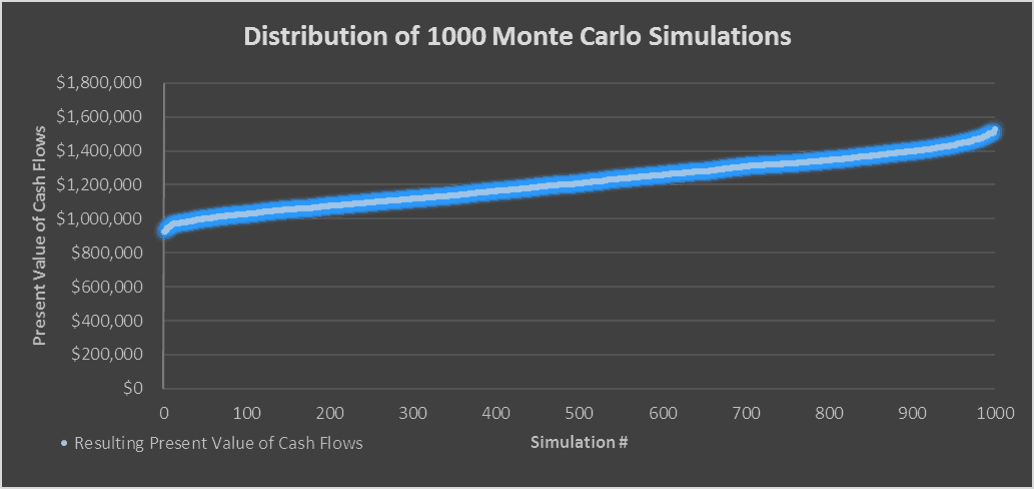
det troliga värdet, med $1.2 miljoner som ”förväntat värde”
det förväntade värdet-vad du kan vara villig att betala
medelvärdet (genomsnittet) av alla simuleringar är ditt ”förväntade värde” eller vad du kan vara villig att betala för ämnesegenskapen med tanke på dina antaganden. I mitt fall är det förväntade värdet cirka 1,2 miljoner dollar.
jag gillar också att beräkna minimi -, Max-och standardavvikelsen för simuleringarna för att få en känsla för värdena. Så till exempel, i det här fallet är minimumet cirka 925 000 dollar och det maximala är cirka 1,5 miljoner dollar. Vad detta betyder är att det fanns en instans där jag skulle behöva betala $925,000 för att träffa en 8% avkastning och det fanns en instans där jag kunde betala $1.5 miljoner för att träffa en 8% avkastning.
men ju fler simuleringar du kör, desto mer kommer värdena att skapa ett normativt mönster där du har en 68% sannolikhet att värdet kommer att vara en standardavvikelse från medelvärdet och en 95% sannolikhet att värdet kommer att vara två standardavvikelser från medelvärdet (68-95-99-regeln). Därför, ju mindre standardavvikelse, desto säkrare kan du vara om ditt förväntade värde.
så Sammanfattningsvis, för vår hypotetiska lägenhetsbyggnad, skulle vi vara villiga att betala någonstans mellan $925,000 och $1.5 miljoner med $1.2 miljoner som det mest troliga inköpspriset.
Video Tutorial – kör Monte Carlo-simuleringar i fastigheter
som ett komplement till den skriftliga handledningen ovan har jag spelat in en video som går igenom att göra dina egna Monte Carlo-simuleringar för fastigheter i Excel.
Följ med att använda Excel-filen från videon
för att göra denna Monte Carlo – simuleringshandledning tillgänglig för alla, erbjuds den på en ”betala vad du kan” – basis utan minimum (ange $0 om du vill) eller maximalt (ditt stöd hjälper till att hålla innehållet kommande-liknande fastighetskursmoduler säljer för $100 – $300+). Ange bara ett pris tillsammans med en e-postadress för att skicka nedladdningslänken till och klicka sedan på ’Fortsätt’. Om du har några frågor om vårt ”Betala vad du kan” – program eller varför vi erbjuder våra modeller på grundval av detta, vänligen kontakta antingen Mike eller Spencer.
född och uppvuxen i nordvästra USA, Spencer Burton har nästan 20 år av bostäder och kommersiella fastigheter erfarenhet. Under sin karriär har han tecknat 30 miljarder dollar av kommersiella fastigheter hos några av de största institutionella fastighetsbolagen i världen. Han är för närvarande chef för fastighetsinvesteringar och medlem i grundarteamet på Stablewood Properties. Spencer har en BS i internationella frågor från Florida State University och en magisterexamen i fastighetsfinansiering från Cornell University.
