Comment exécuter des Simulations Monte Carlo dans Excel
Vous souhaitez donc exécuter des simulations Monte Carlo dans Excel, mais votre projet n’est pas assez volumineux ou vous ne faites pas ce type d’analyse probabiliste assez pour justifier l’achat d’un complément coûteux. Vous êtes au bon endroit. La fonctionnalité intégrée d’Excel permet la modélisation stochastique, y compris l’exécution d’autant de simulations que la puissance de traitement de votre ordinateur le supportera, et ce court article avec tutoriel vidéo vous guide à travers la configuration et le processus d’exécution de simulations Monte Carlo dans Excel sans aucun complément nécessaire.
Analyse probabiliste du point de vue de l’immobilier
Ceci est un blog immobilier commercial, et donc ce tutoriel examine la modélisation stochastique du point de vue d’un professionnel de l’immobilier. Cependant, la grande majorité des techniques présentées dans cet article fonctionneront dans toutes les disciplines.
Je noterai également que plusieurs des concepts présentés ici ont été adaptés de l’excellente thèse de doctorat de Keith Chin-Kee Leung sur le sujet: Au-delà de l’Analyse DCF dans la Modélisation Financière Immobilière: Évaluation Probabiliste des entreprises Immobilières.

Simulations Monte Carlo pour l’Immobilier – Niveau Nerd Excel: 1,000,000
Ce tutoriel n’est pas
Ce post n’est pas un cours sur l’analyse de probabilité. En tant que tel, il suppose que vous avez une compréhension de base des probabilités, des statistiques, d’Excel et que vous savez ce qu’est une simulation de Monte Carlo. Si vous souhaitez vous rafraîchir sur les probabilités ou les statistiques en général, je vous recommande de suivre un cours sur le sujet. Voici un MOOC gratuit (massive open online course) offert par Duke:
- Introduction aux probabilités et aux données
Le Scénario – Un appartement
Avant d’exécuter vos simulations, vous aurez besoin d’un scénario à modéliser. Dans ce cas, nous allons exécuter un flux de trésorerie actualisé de base sur un immeuble hypothétique pour déterminer combien nous serions prêts à payer pour la propriété aujourd’hui. Voici ce que nous savons:
- La propriété en question a 10 unités
- La propriété en question facture 1000 $ / mois pour chaque unité; les loyers ont augmenté de 3% l’an dernier
- Il y a une unité vacante, et pour simplifier, nous supposons qu’il y aura toujours une unité vacante
- Les dépenses sont de 3 000 $ par mois; les dépenses ont augmenté de 2% l’an dernier
- Les propriétés comparables se vendent à un taux de plafonnement de 5,5% à 6,0% aujourd’hui, mais les taux de plafonnement devraient augmenter d’environ 5 points de base par an dans les années à venir (taux de plafonnement de sortie entre 5,75% et 6.25%)
- Prévoyez de conserver la propriété pendant cinq ans
- Visez un rendement non généré de 8%
Configuration du modèle
Ensuite, j’ai configuré mon modèle Excel en prévision de l’exécution des simulations (vous pouvez télécharger le classeur Excel utilisé dans ce tutoriel à la fin de cet article).
- Dans les colonnes B et D, j’abandonne mes hypothèses de base
- Cellule G2 J’étiquette « Valeur DCF »
- À la ligne 14, à partir de la cellule F14 à K14, j’ajoute un en-tête de période avec six périodes dont une période zéro
- Cellule E15 J’étiquette « Loyer »
- Cellule E16 I étiquette « Charges »
- Cellule E17 I étiquette « Résultat d’exploitation net »
- Cellule E18 I étiquette « Valeur Résiduelle »
- Cellule L17 I étiquette « Plafond de sortie »
- Cellule E19 I étiquette « Flux de trésorerie net »
- Cellule D14 I étiquette « Taux de croissance »
- Dans la cellule G15 j’écris la formule: =9*12*$D$4*(1+$D15)^(G14-1), ce qui signifie neuf unités (10 unités moins une vide de l’unité), les temps de 12 mois, de $D$4 (1000$de loyer/unité/mois), temps un plus $D15 (le probable taux de croissance calculé dans la cellule D15), élevé à la période (G15), moins (j’soustraire, car nous ne voulons pas louer à croître dans l’année). Étant donné que les références de cellule absolues appropriées ont été créées (par exemple $D$4 etDD15), je peux ensuite copier la formule directement dans la cellule K15.
- Je suis un processus similaire pour les dépenses, en utilisant la formule: =DD77 * 12 * (1 +$D16) ^ (G14-1) dans la cellule G16, puis en copiant cette formule dans la cellule K16.
- Dans les cellules G17 à K17, je soustrais les dépenses du loyer (par exemple dans G17 j’écris = G15-G16) pour arriver à un résultat d’exploitation net pour chaque année.
- Dans la cellule K18, j’écris la formule: = K17 / L18, ce qui signifie diviser le résultat d’exploitation net de la cinquième année par le taux de plafond de sortie probable (L18).
- Dans les cellules G19 à K19, j’additionne les flux de trésorerie nets pour chaque année : résultat d’exploitation net de la première à la quatrième année et résultat d’exploitation net plus valeur résiduelle de la cinquième année.
- Enfin, dans la cellule G3, je calcule la valeur actualisée du flux de trésorerie de la ligne 19 actualisée à 8% (le rendement cible sans effet de levier) en utilisant la formule: = VAN (D12, G19: K19).
Avec la configuration du DCF, je peux maintenant passer à l’ajout de probabilité à mes hypothèses.
Ajout de probabilité à l’aide de la fonction RANDBETWEEN()
Dans notre scénario ci-dessus, nous avons quelques hypothèses incertaines et seraient donc d’excellents candidats pour ajouter de la variabilité. Tout d’abord, nous devons choisir un type de distribution pour notre probabilité.
Nous avons un certain nombre d’options, les deux plus courantes étant la distribution uniforme (probabilité constante où tous les résultats sont également probables) et la distribution normale (pensez à la probabilité de la courbe en cloche où la valeur résultante est susceptible d’être plus proche de la moyenne). Par souci de simplicité, nous choisirons une distribution uniforme.
- Dans la cellule D15, j’ajoute une variabilité uniforme au taux de croissance des loyers en utilisant la formule: =DD5 5 * RANDBETWEEN (-500,2000) / 1000, ce qui signifie prendre 3% (la croissance des loyers de l’année dernière à partir de la cellule $D5 5) et la multiplier par un nombre aléatoire compris entre -0,5 et 2.0 (RANDBETWEEN (-50 200) / 100) de sorte que le taux de croissance des loyers qui en résulte tombe aléatoirement entre -1,5% et 6,0%.
- Dans la cellule D16, j’ajoute une variabilité uniforme au taux de croissance des dépenses en utilisant une formule similaire: =DD8 8 * RANDBETWEEN (-500,2000) / 1000, seulement dans ce cas, je prends le taux de croissance des dépenses de l’année dernière (2% de la cellule $D8 8) et le multiplie par un nombre aléatoire compris entre -0,5 et 2,0 (RANDBETWEEN (-50,200) / 100) de sorte que le taux de croissance des dépenses résultant diminue aléatoirement entre -1,0% et 4,0%.
- Enfin, dans la cellule L18, j’ajoute une variabilité uniforme au taux de plafond de sortie en utilisant la formule: = D10 * RANDBETWEEN (958,3, 1041,7) / 1000, ce qui signifie prendre 6% (la moyenne entre la fourchette attendue de 5,75% et 6,25% pour les taux de plafond de sortie en cinquième année) et le multiplier par un nombre aléatoire compris entre 0,9583 et 1,0417 (RANDBETWEEN (958,3, 1041,7) / 1000) de sorte que le taux de plafond de sortie résultant tombe aléatoirement entre 5,75% et 6,25%.
Vous verrez maintenant, lorsque vous appuyez sur F9, que les valeurs du taux de croissance des loyers, du taux de croissance des dépenses et du taux de plafond de sortie changent de manière aléatoire, ce qui entraîne une variation aléatoire des flux de trésorerie et de la valeur globale des flux de trésorerie actualisés.
Exécution de simulations Monte Carlo à l’aide de tables de données
Avec une probabilité ajoutée à votre modèle, vous pouvez commencer à exécuter vos simulations Monte Carlo. Ce processus implique la création d’une table de données, liée à votre valeur DCF (G3) afin que chaque simulation enregistre la valeur DCF résultante de cette simulation.
Voici comment nous exécutons les simulations Monte Carlo à l’aide de la fonction de tableau de données dans Excel:
- Cellule B27 Je marque « Simulation # »
- Je lie la cellule C27 à la valeur DCF (= G3)
- Je numérote les cellules B28 à B1027 de 1 à 1000. Pour ce faire, j’ai d’abord mis la cellule B28 à 1. J’entre ensuite la formule = B28 + 1 dans la cellule B29. Enfin, je copie la formule dans B29 dans la cellule B1027.
- Avec les simulations numérotées et la cellule C27 liée à la valeur DCF, je sélectionne les cellules B27 à C1027 et clique sur la fonction « Tableau de données » (Tableau de données > Analyse de simulation >).
- Je laisse la case « Cellule d’entrée de ligne: » vide et clique sur la case « Cellule d’entrée de colonne ». Je sélectionne une cellule vide dans la feuille de calcul (quelle cellule n’a pas d’importance tant que c’est une cellule toujours vide), appuie sur Entrée, puis sur « OK ».
- La table de données sera mise à jour avec 1 000 itérations de notre simulation et le tour est joué : vous avez exécuté une simulation Monte Carlo dans Excel à l’aide de la table de données.
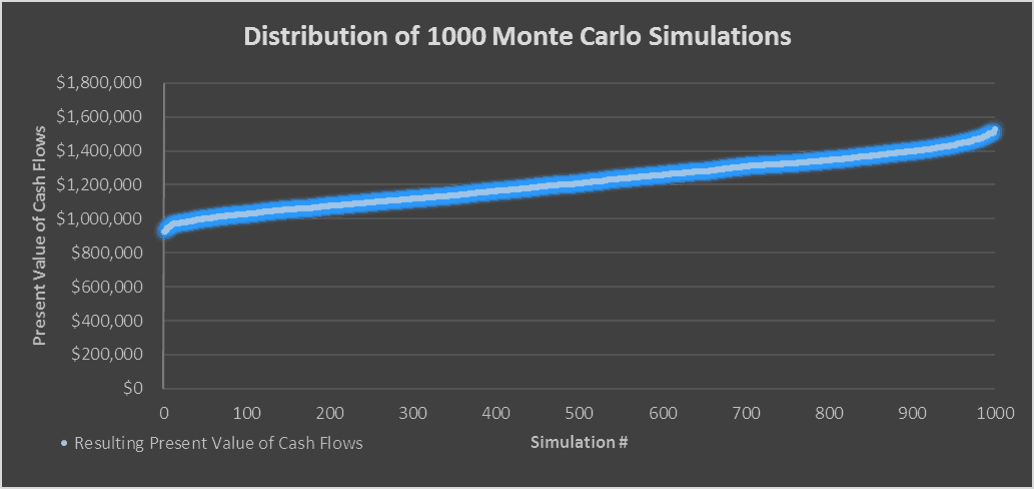
La plage de valeurs probable, 1,2 million de dollars étant la « Valeur attendue » »
La Valeur attendue – Ce que vous pourriez être prêt à Payer
La moyenne (moyenne) de toutes les simulations est votre « Valeur attendue » ou ce que vous pourriez être prêt à payer pour la propriété en question compte tenu de vos hypothèses. Dans mon cas, la valeur attendue est d’environ 1,2 million de dollars.
J’aime aussi calculer le minimum, le maximum et l’écart type des simulations pour avoir une idée de la plage des valeurs. Ainsi, par exemple, dans ce cas, le minimum est d’environ 925 000 $ et le maximum est d’environ 1,5 million de dollars. Cela signifie qu’il y avait un cas où je devrais payer 925 000 $ pour obtenir un rendement de 8% et il y avait un cas où je pouvais payer 1,5 million de dollars pour obtenir un rendement de 8%.
Néanmoins, plus vous exécutez de simulations, plus les valeurs créeront un modèle normatif où vous avez une probabilité de 68% que la valeur soit un écart-type par rapport à la moyenne et une probabilité de 95% que la valeur soit deux écarts-types par rapport à la moyenne (la règle 68-95-99). Par conséquent, plus l’écart type est petit, plus vous pouvez être certain de votre valeur attendue.
Donc, en conclusion, pour notre immeuble hypothétique, nous serions prêts à payer quelque part entre 925 000 $ et 1,5 million de dollars, 1,2 million étant le prix d’achat le plus probable.
Tutoriel vidéo – Exécution de simulations Monte Carlo dans l’immobilier
En complément du tutoriel écrit ci-dessus, j’ai enregistré une vidéo qui vous guide dans vos propres simulations Monte Carlo pour l’immobilier dans Excel.
Suivez le fichier Excel de la vidéo
Pour rendre ce tutoriel de simulation de Monte Carlo accessible à tous, il est offert sur une base « Payez ce que vous pouvez » sans minimum (entrez 0 $ si vous le souhaitez) ou maximum (votre support aide à maintenir le contenu à venir – des modules de cours immobiliers similaires se vendent entre 100 $ et 3003 +). Entrez simplement un prix avec une adresse e-mail à laquelle envoyer le lien de téléchargement, puis cliquez sur « Continuer ». Si vous avez des questions sur notre programme « Payez ce que vous pouvez » ou sur les raisons pour lesquelles nous proposons nos modèles sur cette base, veuillez contacter Mike ou Spencer.
À propos de l’auteur: Né et élevé dans le nord-ouest des États-Unis, Spencer Burton a près de 20 ans d’expérience dans l’immobilier résidentiel et commercial. Au cours de sa carrière, il a souscrit pour 30 milliards de dollars de biens immobiliers commerciaux auprès de certaines des plus grandes sociétés immobilières institutionnelles au monde. Il est actuellement Responsable des investissements immobiliers et membre de l’équipe fondatrice de Stablewood Properties. Spencer est titulaire d’une licence en Affaires internationales de l’Université d’État de Floride et d’une Maîtrise en Finance immobilière de l’Université Cornell.
