kuinka suorittaa Monte Carlo-simulaatioita Excelissä
joten haluat suorittaa Monte Carlo-simulaatioita Excelissä, mutta projektisi ei ole tarpeeksi suuri tai et tee tällaista todennäköisyysanalyysia tarpeeksi, jotta voisit ostaa kalliin lisäosan. Tulit oikeaan paikkaan. Excelin sisäänrakennettu toiminnallisuus mahdollistaa stokastisen mallinnuksen, mukaan lukien simulaatioiden suorittamisen niin monta kertaa kuin tietokoneen prosessointiteho tukee, ja tämä lyhyt viesti opetusvideolla opastaa Monte Carlo-simulaatioiden asennuksen ja suorittamisen Excelissä ilman tarvittavia lisäosia.
Todennäköisyysanalyysi Kiinteistönäkökulmasta
tämä on liikekiinteistöblogi, ja siksi tämä opetusohjelma tarkastelee stokastista mallinnusta kiinteistöalan ammattilaisen näkökulmasta. Kuitenkin, suurin osa tekniikoita esitetty tässä viestissä toimii eri tieteenalojen.
I ’ll also note, some of the concepts shown here I adapted from Keith Chin-Kee Leung’ s excellente graduate on the subject: Beyond DCF Analysis in Real Estate Financial Modeling: Probabilistic Evaluation of Real Estate Ventures.

Monte Carlo Simulations for Real Estate-Excel Nerd Level: 1,000,000
mikä tämä on Tutorial ei ole
tämä viesti ei ole kurssi todennäköisyysanalyysi. Sinällään, se olettaa sinulla on perustiedot Todennäköisyys, Tilastot, Excel, ja tietää, mitä Monte Carlo simulaatio on. Jos haluat saada kertaus todennäköisyys tai tilastot yleensä, suosittelen kurssille aiheesta. Tässä on ilmainen MOOC (massive open online course) tarjoamia Duke:
- Johdanto todennäköisyyteen ja tietoihin
skenaario-asuntokauppa
ennen simulaatioiden suorittamista tarvitset skenaarion mallintamiseen. Tässä tapauksessa laskemme hypoteettiseen kerrostaloon alennetun kassavirran-ja selvitämme, paljonko olemme valmiita maksamaan kiinteistöstä. Tämän me tiedämme:
- subject property has 10 units
- the subject property charges $1000 / kk for per unit; vuokrat kasvavat 3% viime vuonna
- on yksi yksikkö vapaana, ja yksinkertaisuuden vuoksi oletamme, että aina on yksi yksikkö vapaana
- kulut ovat 3000 dollaria kuukaudessa; kulut kasvavat 2% viime vuonna
- vertailukelpoiset kiinteistöt myyvät 5,5% – 6,0% ylärajalla tänään, mutta ylärajan odotetaan kasvavan noin 5 peruspistettä vuodessa tulevina vuosina (poistumiskorko välillä 5,75% ja 6.25%)
- Plan to hold the property for five years
- Target an 8% unvertered return
seting Up the Model
Next, I set up my Excel model in preparation for running the simulations (you can download the Excel workbook used in this tutorial at the end of this post).
- sarakkeeseen B ja D, pudotan perusoletukseni
- solun G2 I etiketti ”DCF-arvo”
- rivillä 14, alkaen solusta F14-K14, lisään jakson otsakkeen, jossa on kuusi jaksoa sisältäen jakson nolla
- solun E15 I etiketti ”vuokra”
- solun E16 i etiketti ”kulu”
- solun E17 I etiketti ”nettotulo”
- solun E18 I etiketti ”jäännösarvo”
- solun L17 I etiketti ”Poistumiskatto”
- solu E19 I label ”nettokassavirta”
- solu D14 I Label ”kasvuvauhti”
- solussa G15 kirjoitan kaavan: =9 * 12 * $d$4 * (1+$D15)^(G14-1) mikä tarkoittaa yhdeksää yksikköä (10 yksikköä vähennettynä yhdellä tyhjällä yksiköllä), kertaa 12 kuukautta, kertaa $D$4 ($1000 vuokra/yksikkö/kuukausi), kertaa yksi plus $D15 (todennäköinen kasvuvauhti laskettu solussa D15), korotettuna jaksoon (G15) miinus yksi (vähennän yhden, koska emme halua vuokran kasvavan ensimmäisenä vuonna). Koska oikea absoluuttinen solu viittaukset on luotu (esim $d$4 ja $D15), voin sitten kopioida kaavan oikeus solu K15.
- seuraan kulujen osalta samanlaista prosessia käyttäen kaavaa: = $D$7 * 12 * (1+$D16)^(G14-1) solussa G16 ja kopioimalla tämän kaavan ulos soluun K16.
- soluissa G17 – K17 vähennän vuokrakulut (esim. luokassa G17 kirjoitan =G15-G16) saadakseni nettotulon kultakin vuodelta.
- soluun K18 kirjoitan kaavan: =K17 / L18, mikä tarkoittaa, että jaetaan vuoden viisi liikevoitto todennäköisellä poistumiskattokertoimella (L18).
- soluissa G19 – K19 I lasketaan yhteen kunkin vuoden nettorahavirrat: liiketoiminnan nettotulot vuosina yhdestä neljään ja liiketoiminnan nettotulot lisättynä jäännösarvolla vuonna viisi.
- lopuksi solussa G3 I lasketaan rivillä 19 olevan kassavirran nykyarvo, joka on diskontattu takaisin 8 prosentilla(tavoitearvo,josta ei ole saatu verovapaata tuottoa), käyttäen kaavaa: =nettonykyarvo (D12, G19:K19).
DCF: n perustamisen myötä voin nyt siirtyä todennäköisyyden lisäämiseen oletuksiini.
lisäämällä todennäköisyys käyttämällä RANDBETWEEN () funktio
meidän skenaario edellä, meillä on pari oletuksia, jotka ovat epävarmoja, ja siksi olisi suuria ehdokkaita lisäämällä vaihtelua. Ensin meidän on valittava jakaumatyyppi todennäköisyydellemme.
meillä on useita vaihtoehtoja, joista kaksi yleisintä ovat yhtenäinen jakauma (jatkuva todennäköisyys, jossa kaikki tulokset ovat yhtä todennäköisiä) ja normaalijakauma (think bell-käyrän todennäköisyys, jossa tuloksena oleva arvo on todennäköisesti lähempänä keskiarvoa). Yksinkertaisuuden vuoksi valitsemme yhtenäisen jakauman.
- solussa D15 lisään tasaisen vaihtelun vuokrien kasvuvauhtiin kaavalla: = $D$5*RANDBETWEEN (-500,2000) / 1000, mikä tarkoittaa ottaa 3% (viime vuoden vuokrien kasvu solusta $D$5) ja moninkertaistaa sen satunnaisluvulla välillä -0,5 ja 2.0(RANDBETWEEN (-50,200) / 100) niin, että tuloksena vuokrien kasvuvauhti putoaa satunnaisesti välillä -1,5% ja 6,0%.
- solussa D16 lisään yhdenmukaisen vaihtelun kulujen kasvuvauhtiin käyttäen samanlaista kaavaa: =$D$8*RANDBETWEEN(-500,2000)/1000, vain tässä tapauksessa otan viime vuoden kulujen kasvuvauhdin (2% solusta $D$8) ja kerron sen satunnaisluvulla välillä -0,5-2,0 (RANDBETWEEN(-50,200)/100) niin, että tuloksena oleva kulujen kasvuvauhti osuu satunnaisesti-1,0% ja 4,0%.
- lopuksi, solussa L18, lisään tasaisen vaihtelun poistumisnopeuteen käyttäen kaavaa: =D10*RANDBETWEEN(958.3,1041.7)/1000, mikä tarkoittaa ottaa 6% (keskiarvo välillä 5.75% ja 6.25% odotetun vaihteluvälin exit cap rates vuonna viisi) ja moninkertaistaa sen satunnaisluvulla välillä 0.9583 ja 1.0417 (RANDBETWEEN(958.3,1041.7)/1000) siten, että tuloksena exit cap ratio putoaa satunnaisesti välillä 5.75% ja 6.25%.
näet nyt, kun painat F9: ää, että vuokrien kasvuvauhti, kulujen kasvuvauhti ja poistumiskoron arvot muuttuvat satunnaisesti, jolloin kassavirrat ja diskontattu kokonaisrahavirta-arvo muuttuvat satunnaisesti.
ajamalla Monte Carlo-simulaatioita käyttäen Datataulukoita
ja lisäämällä todennäköisyys malliisi, voit aloittaa Monte Carlo-simulaatioiden ajamisen. Tähän prosessiin kuuluu datataulukon rakentaminen, joka liittyy DCF-arvoosi (G3) siten, että jokainen simulaatio tallentaa tuloksena olevan DCF-arvon kyseisestä simulaatiosta.
näin suoritamme Monte Carlon simulaatiot Excelin Datataulukko-ominaisuuden avulla:
- solun B27 I etiketti ”simulaatio #”
- I linkittää solun C27 DCF-arvoon (=G3)
- I numerosolut B28 – B1027 1-1000. Tätä varten asetin ensin solun B28 arvoon 1. Seuraavaksi syötän kaavan =B28+1 soluun B29. Lopuksi, kopioin kaavan B29 alas solu b1027.
- kun simulaatiot on numeroitu ja solu C27 liitetty DCF-arvoon, valitsen solut B27 – C1027 ja napsautan ”Datataulukko” -ominaisuutta (Data>mitä-jos-analyysi>Datataulukko).
- jätän ”rivin syötekenno:” – ruudun tyhjäksi ja napsautan ”sarakkeen syötekenno” – ruutua. Valitsen tyhjän solun laskentataulukossa (mikä solu ei ole väliä niin kauan kuin se on solu, joka on aina tyhjä), paina enter, ja sitten ”OK”.
- datataulukko päivittyy 1 000 simulaatiomme iteraatiolla ja voila you ’ ve run a Monte Carlo simulation in Excel using the data table.
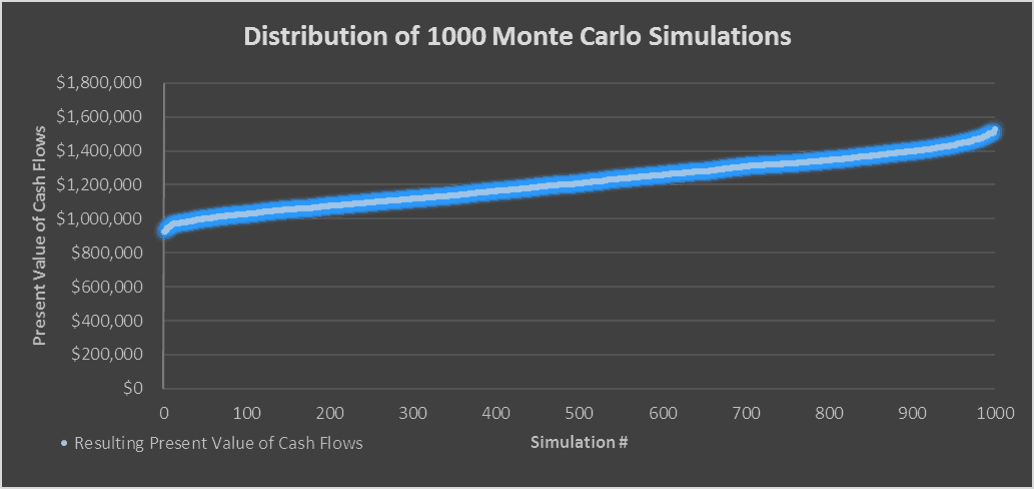
todennäköinen arvojen vaihteluväli, 1,2 miljoonaa dollaria on ”odotusarvo”
odotusarvo-mitä saatat olla valmis maksamaan
kaikkien simulaatioiden keskiarvo on sinun ”Odotusarvosi” tai mitä saatat olla valmis maksamaan kohteen omaisuudesta olettamustesi perusteella. Minun tapauksessani odotusarvo on noin 1,2 miljoonaa dollaria.
haluan myös laskea simulaatioiden minimi -, maksimi-ja keskihajonnan saadakseni tuntumaa arvojen vaihteluväliin. Eli esimerkiksi tässä tapauksessa minimi on noin 925 000 dollaria ja maksimi noin 1,5 miljoonaa dollaria. Mitä tämä tarkoittaa, että oli esimerkiksi, jossa minun pitäisi maksaa $925,000 jotta osuma 8% tuotto ja siellä oli esimerkiksi, jossa voisin maksaa $1.5 miljoonaa osua 8% tuotto.
kuitenkin, mitä enemmän simulaatioita suoritetaan, sitä enemmän arvot luovat normatiivisen kuvion, jossa on 68% todennäköisyys, että arvo on yksi keskihajonta keskiarvosta ja 95% todennäköisyys, että arvo on kaksi keskihajontaa keskiarvosta (68-95-99-sääntö). Siksi, mitä pienempi keskihajonta, sitä varmempi voit olla odotusarvostasi.
joten yhteenvetona, hypoteettisesta kerrostalostamme olisimme valmiita maksamaan jotain 925 000-1,5 miljoonaa dollaria ja 1,2 miljoonaa dollaria on todennäköisin kauppahinta.
Video Tutorial – Running Monte Carlo Simulations in Real Estate
yllä olevan kirjoitetun opetusohjelman täydennyksenä olen tallentanut videon, joka kävelee läpi tehden omia Monte Carlo simulaatioita kiinteistöille Excelissä.
seuraa mukana käyttämällä Excel-tiedoston Video
jotta tämä Monte Carlo simulointi opetusohjelma saatavilla kaikille, se tarjotaan ”maksa mitä pystyt” perusteella ilman minimiä (kirjoita $0 jos haluat) tai maksimi (tuki auttaa pitämään sisällön tulossa – samanlaisia kiinteistö kurssi moduulit myydä $100 – $300+). Syötä vain hinta yhdessä sähköpostiosoitteen kanssa, johon latauslinkki lähetetään, ja napsauta sitten ’Jatka’. Jos sinulla on kysyttävää ”maksa mitä pystyt” – ohjelmastamme tai siitä, miksi tarjoamme mallejamme tällä perusteella, ota yhteyttä joko Mikeen tai Spenceriin.
kirjoittajasta: syntynyt ja kasvanut Luoteis-Yhdysvalloissa, Spencer Burtonilla on lähes 20 vuoden kokemus asuin-ja liikekiinteistöistä. Uransa aikana hän on kuitannut 30 miljardin dollarin edestä liikekiinteistöjä eräissä maailman suurimmista institutionaalisista kiinteistöyhtiöistä. Hän on tällä hetkellä kiinteistösijoitusjohtaja ja Stablewood Propertiesin perustajaryhmän jäsen. Spencerillä on kansainvälisten asioiden BS Floridan osavaltionyliopistosta ja Masters Kiinteistörahoituksesta Cornellin yliopistosta.
