Ausführen von Monte-Carlo-Simulationen in Excel
Sie möchten also Monte-Carlo-Simulationen in Excel ausführen, aber Ihr Projekt ist nicht groß genug oder Sie führen diese Art der probabilistischen Analyse nicht aus genug, um den Kauf eines teuren Add-Ins zu rechtfertigen. Nun, Sie sind an der richtigen Stelle. Die integrierte Funktionalität von Excel ermöglicht die stochastische Modellierung, einschließlich der Ausführung so vieler Simulationen, wie die Rechenleistung Ihres Computers unterstützt, und dieser kurze Beitrag mit Video-Tutorial führt Sie durch das Setup und den Prozess der Ausführung von Monte-Carlo-Simulationen in Excel, ohne dass Add-Ins erforderlich sind.
Probabilistische Analyse aus Immobilienperspektive
Dies ist ein Blog für Gewerbeimmobilien, und daher befasst sich dieses Tutorial mit stochastischer Modellierung aus der Perspektive eines Immobilienfachmanns. Die große Mehrheit der in diesem Beitrag gezeigten Techniken funktioniert jedoch disziplinübergreifend.
Ich werde auch bemerken, einige der hier gezeigten Konzepte habe ich aus Keith Chin-Kee Leungs exzellenter Diplomarbeit zum Thema: Beyond DCF Analysis in Real Estate Financial Modeling: Probabilistic Evaluation of Real Estate Ventures .

Monte Carlo Simulationen für Immobilien – Excel Nerd Level: 1,000,000
Was dies ist Tutorial ist nicht
Dieser Beitrag ist kein Kurs zur Wahrscheinlichkeitsanalyse. Daher wird davon ausgegangen, dass Sie ein grundlegendes Verständnis von Wahrscheinlichkeit, Statistik und Excel haben und wissen, was eine Monte-Carlo-Simulation ist. Wenn Sie eine Auffrischung über Wahrscheinlichkeit oder Statistik im Allgemeinen erhalten möchten, empfehle ich einen Kurs zu diesem Thema. Hier ist ein kostenloser MOOC (Massive Open Online Course) von Duke:
- Einführung in Wahrscheinlichkeit und Daten
Das Szenario – Ein Apartment Deal
Bevor Sie Ihre Simulationen ausführen, benötigen Sie ein Szenario zum Modellieren. In diesem Fall werden wir einen grundlegenden diskontierten Cashflow für ein hypothetisches Wohnhaus durchführen, um festzustellen, wie viel wir heute für die Immobilie bezahlen würden. Hier ist, was wir wissen:
- Die Betreff-Eigenschaft hat 10 Einheiten
- Die Betreff-Eigenschaft berechnet $ 1000 / Monat für jede Einheit; die Mieten steigen im vergangenen Jahr um 3%
- Es ist eine Einheit frei, und der Einfachheit halber gehen wir davon aus, dass es immer eine Einheit frei geben wird
- Die Ausgaben belaufen sich auf 3.000 USD pro Monat; Die Ausgaben steigen im vergangenen Jahr um 2%
- Vergleichbare Immobilien werden heute für eine Obergrenze von 5,5% bis 6,0% verkauft, aber die Obergrenzen werden in den kommenden Jahren voraussichtlich um etwa 5 Basispunkte pro Jahr steigen (Exit–Cap-Rate zwischen 5,75% und 6.25%)
- Planen Sie, die Immobilie für fünf Jahre zu halten
- Zielen Sie auf eine nicht gemanagte Rendite von 8% ab
Einrichten des Modells
Als nächstes habe ich mein Excel-Modell eingerichtet, um die Simulationen auszuführen (Sie können die in diesem Lernprogramm verwendete Excel-Arbeitsmappe am Ende dieses Beitrags herunterladen).
- In Spalte B und D lasse ich meine Basisannahmen fallen
- Zelle G2 Ich beschrifte „DCF-Wert“
- In Zeile 14 füge ich ab Zelle F14 bis K14 einen Periodenkopf mit sechs Perioden hinzu, einschließlich einer Periode Null
- Zelle E15 Ich beschrifte „Miete“
- Zelle E16 I Bezeichnung „Aufwand“
- Zelle E17 I Bezeichnung „Nettobetriebsertrag“
- Zelle E18 I Bezeichnung „Restwert“
- Zelle L17 I Bezeichnung „Exit Cap“
- Zelle E19 I Bezeichnung „Netto-Cashflow“
- Zelle D14 I Bezeichnung „Wachstumsrate“
- In Zelle G15 schreibe ich die Formel: = 9 * 12 * $ D $ 4 * (1 + $ D15) ^ (G14-1) was neun Einheiten bedeutet (10 Einheiten abzüglich einer freien Einheit), mal 12 Monate, mal $ D $ 4 ($ 1000 Miete / Einheit / Monat), mal eins plus $ D15 (die wahrscheinliche Wachstumsrate, berechnet in Zelle D15), erhöht auf die Periode (G15) minus eins (ich subtrahiere eins, weil wir nicht wollen, dass die Miete im ersten Jahr wächst). Da die richtigen absoluten Zellreferenzen erstellt wurden (z. B. $ D $ 4 und $ D15), kann ich die Formel dann direkt in Zelle K15 kopieren.
- Ich folge einem ähnlichen Prozess für Ausgaben und verwende die Formel: = $ D $ 7 * 12 * (1 + $ D16) ^ (G14-1) in Zelle G16 und kopiere diese Formel dann in Zelle K16.
- In den Zellen G17 bis K17 subtrahiere ich die Ausgaben von der Miete (z. B. schreibe ich in G17 =G15-G16), um für jedes Jahr ein Betriebsergebnis zu erzielen.
- In Zelle K18 schreibe ich die Formel: =K17 / L18, was bedeutet, dass das Nettobetriebsergebnis des Jahres fünf durch die wahrscheinliche Exit-Cap-Rate (L18) dividiert wird.
- In den Zellen G19 bis K19 addiere ich die Netto-Cashflows für jedes Jahr: Betriebsergebnis in den Jahren eins bis vier und Betriebsergebnis plus Restwert im fünften Jahr.
- Schließlich berechne ich in Zelle G3 den Barwert des Cashflow-Streams in Zeile 19, der mit 8% (der nicht verschuldeten Zielrendite) abgezinst wird, unter Verwendung der Formel: =NPV (D12, G19:K19).
Mit der DCF-Einrichtung kann ich nun meine Annahmen um Wahrscheinlichkeiten erweitern.
Hinzufügen der Wahrscheinlichkeit mit der Funktion RANDBETWEEN()
In unserem obigen Szenario haben wir einige Annahmen, die unsicher sind und daher gute Kandidaten für das Hinzufügen von Variabilität wären. Zuerst müssen wir einen Verteilungstyp für unsere Wahrscheinlichkeit auswählen.
Wir haben eine Reihe von Optionen, die beiden häufigsten sind die gleichmäßige Verteilung (konstante Wahrscheinlichkeit, bei der alle Ergebnisse gleich wahrscheinlich sind) und die Normalverteilung (denken Sie an die Glockenkurvenwahrscheinlichkeit, bei der der resultierende Wert wahrscheinlich näher am Mittelwert liegt). Der Einfachheit halber wählen wir eine einheitliche Verteilung.
- In Zelle D15 addiere ich der Mietwachstumsrate eine gleichmäßige Variabilität mit der Formel: = $ D $ 5 * RANDBETWEEN(-500,2000) / 1000, was bedeutet, nehmen Sie 3% (Mietwachstum des letzten Jahres aus Zelle $ D $ 5) und multiplizieren Sie es mit einer Zufallszahl zwischen -0.5 und 2.0 (RANDBETWEEN(-50,200) /100), so dass die resultierende Mietwachstumsrate zufällig zwischen -1.5% und 6.0% fällt.
- In Zelle D16 füge ich der Kostenwachstumsrate eine einheitliche Variabilität hinzu, indem ich eine ähnliche Formel verwende: = $ D $ 8 * RANDBETWEEN(-500,2000) / 1000, nur in diesem Fall nehme ich die Kostenwachstumsrate des letzten Jahres (2% aus Zelle $ D $ 8) und multipliziere sie mit einer Zufallszahl zwischen -0.5 und 2.0 (RANDBETWEEN(-50,200) / 100), so dass die resultierende Kostenwachstumsrate zufällig zwischen -1,0% und 4,0%.
- Schließlich füge ich in Zelle L18 der Exit-Cap-Rate unter Verwendung der Formel eine gleichmäßige Variabilität hinzu: = D10 * RANDBETWEEN (958.3,1041.7) / 1000, was bedeutet, nehmen Sie 6% (der Durchschnitt zwischen den erwarteten 5.75% und 6.25% für Exit-Cap-Raten im fünften Jahr) und multiplizieren Sie ihn mit einer Zufallszahl zwischen 0.9583 und 1.0417 (RANDBETWEEN (958.3,1041.7) / 1000), so dass die resultierende Exit-Cap-Rate zufällig zwischen 5.75% und 6.25% fällt%.
Sie werden jetzt sehen, wenn Sie F9 drücken, dass sich die Werte für die Mietwachstumsrate, die Kostenwachstumsrate und die Exit-Cap-Rate zufällig ändern, was zu einer zufälligen Änderung der Cashflows und des gesamten diskontierten Cashflow-Werts führt.
Ausführen von Monte-Carlo-Simulationen mithilfe von Datentabellen
Wenn Ihrem Modell die Wahrscheinlichkeit hinzugefügt wurde, können Sie mit der Ausführung Ihrer Monte-Carlo-Simulationen beginnen. Bei diesem Prozess wird eine Datentabelle erstellt, die mit Ihrem DCF-Wert (G3) verknüpft ist, sodass jede Simulation den resultierenden DCF-Wert aus dieser Simulation aufzeichnet.
So führen wir die Monte-Carlo-Simulationen mit der Datentabellenfunktion in Excel aus:
- Zelle B27 I beschriften Sie „Simulation #“
- I verknüpfen Sie Zelle C27 mit dem DCF-Wert (=G3)
- I Nummerieren Sie die Zellen B28 bis B1027 von 1 bis 1000. Dazu setze ich zuerst Zelle B28 auf 1. Als nächstes gebe ich die Formel = B28 + 1 in Zelle B29 ein. Zuletzt kopiere ich die Formel in B29 in Zelle B1027.
- Wenn die Simulationen nummeriert und Zelle C27 mit dem DCF-Wert verknüpft sind, wähle ich die Zellen B27 bis C1027 aus und klicke auf die Funktion ‚Datentabelle‘ (Daten > Was-wäre-wenn-Analyse > Datentabelle).
- Ich lasse das Feld ‚Zeileneingabezelle:‘ leer und klicke auf das Feld ‚Spalteneingabezelle‘. Ich wähle eine leere Zelle im Arbeitsblatt aus (welche Zelle spielt keine Rolle, solange es sich um eine Zelle handelt, die immer leer ist), drücke die Eingabetaste und dann ‚OK‘.
- Die Datentabelle wird mit 1.000 Iterationen unserer Simulation aktualisiert und voila, Sie haben eine Monte-Carlo-Simulation in Excel mit der Datentabelle ausgeführt.
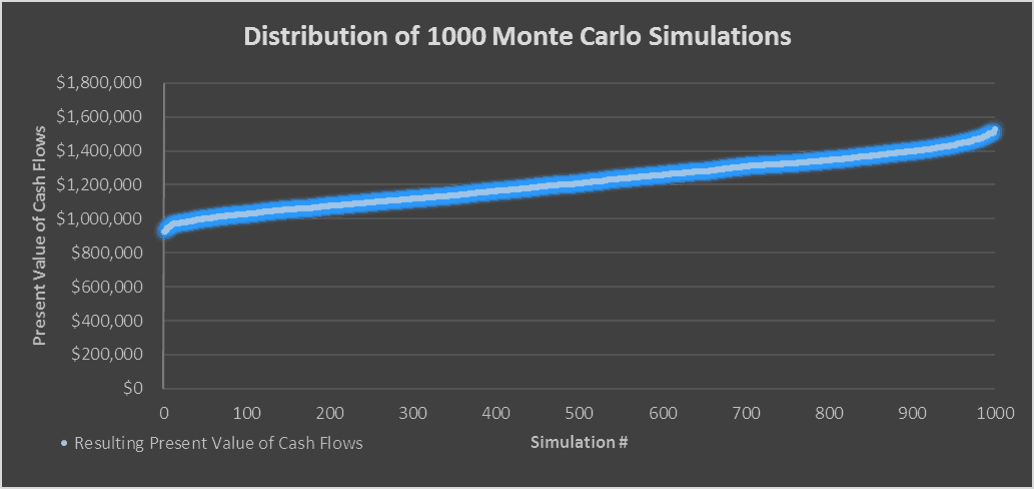
Der wahrscheinliche Wertebereich mit 1,2 Millionen US-Dollar als „erwartetem Wert“
Der erwartete Wert – Was Sie möglicherweise bereit sind zu zahlen
Der Mittelwert (Durchschnitt) aller Simulationen ist Ihr „Erwartungswert“ oder was Sie möglicherweise bereit sind, für die betreffende Eigenschaft unter Ihren Annahmen zu zahlen. In meinem Fall liegt der erwartete Wert bei etwa 1,2 Millionen US-Dollar.
Ich möchte auch das Minimum, Maximum und die Standardabweichung der Simulationen berechnen, um ein Gefühl für den Bereich der Werte zu bekommen. In diesem Fall liegt das Minimum beispielsweise bei 925.000 US-Dollar und das Maximum bei 1,5 Millionen US-Dollar. Dies bedeutet, dass es einen Fall gab, in dem ich 925.000 US-Dollar zahlen musste, um eine Rendite von 8% zu erzielen, und es gab einen Fall, in dem ich 1,5 Millionen US-Dollar zahlen konnte, um eine Rendite von 8% zu erzielen.
Je mehr Simulationen Sie jedoch ausführen, desto mehr erzeugen die Werte ein normatives Muster, bei dem Sie eine Wahrscheinlichkeit von 68% haben, dass der Wert eine Standardabweichung vom Mittelwert und eine Wahrscheinlichkeit von 95% ist, dass der Wert zwei Standardabweichungen vom Mittelwert aufweist (die 68-95-99-Regel). Je kleiner die Standardabweichung ist, desto sicherer können Sie also über Ihren erwarteten Wert sein.
Zusammenfassend wären wir für unser hypothetisches Wohnhaus bereit, irgendwo zwischen 925.000 und 1,5 Millionen US-Dollar zu zahlen, wobei 1,2 Millionen US-Dollar der wahrscheinlichste Kaufpreis sind.
Video-Tutorial – Ausführen von Monte-Carlo-Simulationen in Immobilien
Als Ergänzung zu dem oben beschriebenen Tutorial habe ich ein Video aufgenommen, in dem Sie Ihre eigenen Monte-Carlo-Simulationen für Immobilien in Excel durchführen.
Folgen Sie mit der Excel-Datei aus dem Video
Um dieses Monte Carlo Simulation Tutorial für jedermann zugänglich zu machen, wird es auf einer „Pay What You’re Able“ –Basis ohne Minimum (geben Sie $ 0 ein, wenn Sie möchten) oder Maximum (Ihre Unterstützung hilft, den Inhalt kommen zu lassen – ähnliche Immobilienkursmodule verkaufen für $ 100 – $ 300 +). Geben Sie einfach einen Preis zusammen mit einer E-Mail-Adresse ein, an die Sie den Download-Link senden möchten, und klicken Sie dann auf ‚Weiter‘. Wenn Sie Fragen zu unserem Programm „Pay What You’re Able“ haben oder warum wir unsere Modelle auf dieser Basis anbieten, wenden Sie sich bitte an Mike oder Spencer.
Über den Autor: Spencer Burton ist im Nordwesten der USA geboren und aufgewachsen und verfügt über fast 20 Jahre Erfahrung in Wohn- und Gewerbeimmobilien. Im Laufe seiner Karriere hat er bei einigen der größten institutionellen Immobilienunternehmen der Welt Gewerbeimmobilien im Wert von 30 Milliarden US-Dollar gezeichnet. Derzeit ist er Head of Real Estate Investments und Mitglied des Gründungsteams von Stablewood Properties. Spencer hat einen BS in internationalen Angelegenheiten von der Florida State University und einen Master in Immobilienfinanzierung von der Cornell University.
