Sådan køres Monte Carlo simuleringer i Monte Carlo simuleringer
så du vil køre Monte Carlo simuleringer i Monte Carlo simuleringer, men dit projekt er ikke stort nok, eller du gør ikke denne type probabilistisk analyse nok til at berettige at købe et dyrt tilføjelsesprogram. Nå, du er kommet til det rigtige sted. Den indbyggede funktionalitet giver mulighed for stokastisk modellering, herunder at køre så mange simuleringer, som din computers processorkraft understøtter, og dette korte indlæg med videotutorial fører dig gennem opsætningen og processen med at køre Monte Carlo-simuleringer uden nogen tilføjelser nødvendige.
probabilistisk analyse fra et Ejendomsperspektiv
dette er en kommerciel ejendomsblog, og derfor ser denne tutorial på stokastisk modellering ud fra en ejendomsprofessionel. Imidlertid, det store flertal af teknikkerne vist i dette indlæg vil arbejde på tværs af discipliner.
jeg vil også bemærke, at flere af de begreber, der er vist her, Jeg tilpassede fra Keith Chin-Kee Leungs fremragende kandidatafhandling om emnet: Beyond DCF-analyse i Real Estate Financial Modeling: probabilistisk evaluering af Real Estate Ventures.

Monte Carlo simuleringer til fast ejendom-udmærke Nørd niveau: 1,000,000
hvad dette er Tutorial er ikke
dette indlæg er ikke et kursus om sandsynlighedsanalyse. Som sådan antager det, at du har en grundlæggende forståelse af sandsynlighed, statistik, udmærke sig og vide, hvad en Monte Carlo-simulering er. Hvis du gerne vil have en genopfriskning af sandsynlighed eller statistik generelt, anbefaler jeg at tage et kursus om emnet. Her er et gratis MOOC (massive open online course), der tilbydes af Duke:
- Introduktion til Sandsynlighed og Data
scenariet – en Lejlighedsaftale
før du kører dine simuleringer, skal du bruge et scenario til at modellere. I dette tilfælde vil vi køre en grundlæggende diskonteret pengestrøm på en hypotetisk lejlighedsbygning for at bestemme, hvor meget vi ville være villige til at betale for ejendommen i dag. Her er hvad vi ved:
- emnet ejendom har 10 enheder
- emnet ejendom opkræver $1000 / måned for hver enhed; huslejen vokser med 3% sidste år
- der er en enhed ledig, og for enkelhedens skyld antager vi, at der altid vil være en enhed ledig
- udgifterne er $3.000 pr.måned; udgifterne vokser med 2% sidste år
- sammenlignelige ejendomme sælger for en 5.5% – 6.0% cap sats i dag, men cap satser forventes at vokse med omkring 5 basispoint om året i de kommende år (Afslut cap sats mellem 5.75% og 6.25%)
- planlægger at holde ejendommen i fem år
- Målret mod et 8% uleveraged afkast
opsætning af modellen
dernæst konfigurerer jeg min model som forberedelse til at køre simuleringerne (du kan hente projektmappen, der bruges i denne tutorial i slutningen af dette indlæg).
- i kolonne B og D falder jeg i mine basisforudsætninger
- celle G2 jeg mærker “DCF-værdi”
- i række 14, startende i celle F14 til K14, tilføjer jeg en periodeoverskrift med seks perioder inklusive en periode nul
- celle E15 jeg mærker “leje”
- celle E16 i etiket “udgift”
- celle E17 i etiket “netto driftsindtægter”
- celle E18 I etiket “restværdi”
- celle L17 i etiket “Udgangsdæksel”
- celle E19 i label “netto likviditet”
- celle D14 I etiket “vækstrate”
- i celle G15 skriver jeg formlen: =9 * 12*$D$4 * (1+$D15)^(G14-1), hvilket betyder ni enheder (10 enheder mindre en ledig enhed), gange 12 måneder, gange $D$4 ($1000 leje/enhed/måned), gange en plus $D15 (den sandsynlige vækstrate beregnet i celle D15), hævet til perioden (G15) minus en (jeg trækker en, fordi vi ikke ønsker, at huslejen skal vokse i år et). $D$4 og $D15), kan jeg derefter kopiere formlen ret til celle K15.
- jeg følger en lignende proces for udgifter ved hjælp af formlen: =$D$7*12*(1+$D16)^(G14-1) i celle G16 og kopierer derefter formlen ud til celle K16.
- i celler G17 til K17 trækker jeg udgifter fra husleje (f.eks. i G17 skriver jeg =G15-G16) for at nå frem til en nettodriftsindkomst for hvert år.
- i celle K18 skriver jeg formlen: =K17/L18, hvilket betyder divider år fem nettodriftsindtægter med den sandsynlige Udgangsfrekvens (L18).
- i celler G19 til K19 lægger jeg nettopengestrømme op for hvert år: nettodriftsindtægter i år et til fire og nettodriftsindtægter plus restværdi i år fem.
- endelig beregner jeg i celle G3 nutidsværdien af pengestrømsstrømmen i række 19 diskonteret tilbage til 8% (målet ikke-gearet afkast) ved hjælp af formlen: =NPV(D12, G19:K19).
med DCF-opsætningen kan jeg nu gå videre til at tilføje Sandsynlighed til mine antagelser.
tilføjelse af sandsynlighed ved hjælp af funktionen RANDMELLEM ()
i vores scenarie ovenfor har vi et par antagelser, der er usikre, og derfor ville være gode kandidater til at tilføje variation til. Først skal vi vælge en distributionstype for vores Sandsynlighed.
vi har en række muligheder, hvor de to mest almindelige er ensartet fordeling (konstant Sandsynlighed, hvor alle resultater er lige sandsynlige) og normalfordeling (tænk klokkekurve Sandsynlighed, hvor den resulterende værdi sandsynligvis vil være tættere på gennemsnittet). For enkelhedens skyld vælger vi en ensartet fordeling.
- i celle D15 tilføjer jeg ensartet variabilitet til lejevæksten ved hjælp af formlen: =$D$5*RANDMELLEM(-500,2000)/1000, hvilket betyder at tage 3% (sidste års lejevækst fra celle $D$5) og multiplicere det med et tilfældigt tal mellem -0,5 og 2.0 (RANDMELLEM (-50.200) / 100), så den resulterende lejevæksthastighed falder tilfældigt mellem -1,5% og 6,0%.
- i celle D16 tilføjer jeg ensartet variabilitet til udgiftsvæksthastigheden ved hjælp af en lignende formel: =$D$8*RANDMELLEM(-500,2000)/1000, kun i dette tilfælde tager jeg sidste års udgiftsvæksthastighed (2% fra celle $D$8) og multiplicerer den med et tilfældigt tal mellem -0,5 og 2,0 (RANDMELLEM(-50,200)/100), så den resulterende udgiftsvæksthastighed falder tilfældigt mellem -1,0% og 4,0%.
- endelig tilføjer jeg i celle L18 ensartet variabilitet til udgangshættehastigheden ved hjælp af formlen: =D10*RANDMELLEM(958,3, 1041,7)/1000, hvilket betyder at tage 6% (gennemsnittet mellem 5, 75% og 6, 25% forventet interval for udgangsdækningshastigheder i år fem) og multiplicere det med et tilfældigt tal mellem 0, 9583 og 1, 0417 (RANDMELLEM(958, 3, 1041, 7)/1000), så den resulterende udgangsdækningshastighed falder tilfældigt mellem 5, 75% og 6, 25%.
du vil nu se, når du trykker på F9, at huslejevæksten, udgiftsvæksthastigheden og afslut cap rate-værdierne ændres tilfældigt, hvilket resulterer i en tilfældig ændring i pengestrømmene og den samlede diskonterede pengestrømsværdi.
kører Monte Carlo simuleringer ved hjælp af datatabeller
med Sandsynlighed tilføjet til din model, kan du begynde at køre dine Monte Carlo simuleringer. Denne proces involverer opbygning af en datatabel, der er knyttet til din DCF-værdi (G3), så hver simulering registrerer den resulterende DCF-værdi fra denne simulering.
Sådan kører vi Monte Carlo-simuleringerne ved hjælp af Datatabelfunktionen:
- celle B27 jeg mærker “Simulering #”
- jeg forbinder celle C27 til DCF-værdien (=G3)
- jeg nummererer celler B28 til B1027 fra 1 til 1000. For at gøre dette satte jeg først celle B28 til 1. Jeg indtaster derefter formlen =B28 + 1 i celle B29. Endelig kopierer jeg formlen i B29 ned til celle B1027.
- med simuleringerne nummereret og celle C27 knyttet til DCF-værdien vælger jeg celler B27 til C1027 og klikker på ‘Datatabel’-funktionen (Data>hvad-hvis-analyse> Datatabel).
- jeg lader feltet ‘rækkeindgangscelle:’ være tomt og klikker på feltet ‘Kolonneindgangscelle’. Jeg vælger en tom celle i regnearket (hvilken celle betyder ikke noget, så længe det er en celle, der altid er tom), tryk på enter og derefter ‘OK’.
- datatabellen opdateres med 1.000 gentagelser af vores simulering og voila.
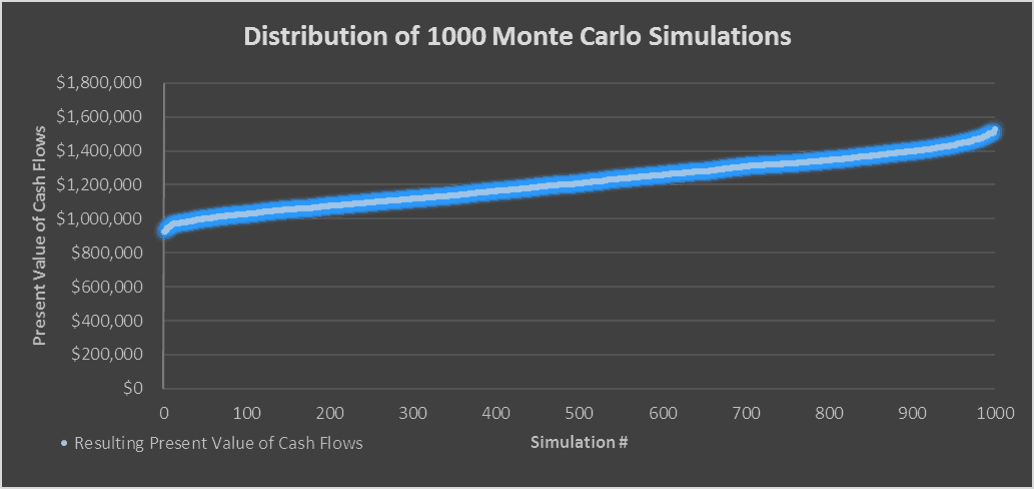
det sandsynlige værdiområde, hvor $1,2 millioner er den “forventede værdi”
den forventede værdi-hvad du måske er villig til at betale
middelværdien (gennemsnittet) af alle simuleringerne er din “forventede værdi” eller hvad du måske er villig til at betale for emnet ejendom givet dine antagelser. I mit tilfælde er den forventede værdi omkring $1,2 millioner.
jeg kan også godt lide at beregne simuleringernes minimum, maksimum og standardafvigelse for at få en fornemmelse af værdiernes rækkevidde. Så for eksempel i dette tilfælde er minimumet omkring $925.000, og maksimum er omkring $1,5 millioner. Hvad dette betyder er, at der var et tilfælde, hvor jeg skulle betale $925.000 for at ramme et afkast på 8%, og der var et tilfælde, hvor jeg kunne betale $1,5 millioner for at ramme et afkast på 8%.
ikke desto mindre, jo flere simuleringer du kører, jo mere vil værdierne skabe et normativt mønster, hvor du har en 68% Sandsynlighed for, at værdien vil være en standardafvigelse fra gennemsnittet og en 95% sandsynlighed for, at værdien vil være to standardafvigelser fra gennemsnittet (68-95-99-reglen). Derfor, jo mindre standardafvigelsen er, desto mere sikker Kan du være på din forventede værdi.
så afslutningsvis, for vores hypotetiske lejlighedsbygning, ville vi være villige til at betale et sted mellem $925.000 og $1,5 millioner med $1,2 millioner er den mest sandsynlige købspris.
Video Tutorial – kører Monte Carlo simuleringer i fast ejendom
som et supplement til den skriftlige tutorial ovenfor, Jeg har optaget en video, der går gennem at gøre dine egne Monte Carlo simuleringer for fast ejendom i udmærke.
for at gøre denne Monte Carlo simulation tutorial tilgængelig for alle, tilbydes den på en “Betal hvad du kan” basis uden minimum (indtast $0, hvis du vil) eller maksimum (din support hjælper med at holde indholdet kommer – lignende real estate kursus moduler sælge for $100 – $300+). Du skal blot indtaste en pris sammen med en e-mail-adresse for at sende Hent linket til, og klik derefter på ‘Fortsæt’. Hvis du har spørgsmål om vores “Betal hvad du kan” – program, eller hvorfor vi tilbyder vores modeller på dette grundlag, kontakt enten Mike eller Spencer.
om forfatteren: født og opvokset i det nordvestlige USA, Spencer Burton har næsten 20 års erfaring med boliger og erhvervsejendomme. I løbet af sin karriere har han tegnet 30 milliarder dollars erhvervsejendomme hos nogle af de største institutionelle ejendomsfirmaer i verden. Han er i øjeblikket leder af ejendomsinvesteringer og medlem af grundlæggelsesteamet hos . Spencer har en BS i Internationale Anliggender fra Florida State University og en kandidatgrad i ejendomsfinansiering fra Cornell University.
om forfatteren: født og opvokset i det nordvestlige USA, Spencer Burton har næsten 20 års erfaring med boliger og erhvervsejendomme. I løbet af sin karriere har han tegnet 30 milliarder dollars erhvervsejendomme hos nogle af de største institutionelle ejendomsfirmaer i verden. Han er i øjeblikket leder af ejendomsinvesteringer og medlem af grundlæggelsesteamet hos
